弾性変形と塑性変形
弾性変形
弾性変形とは
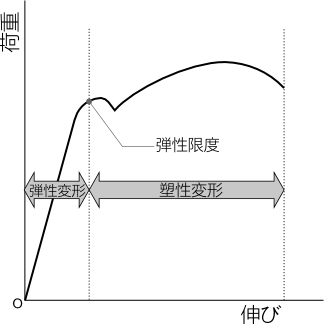
荷重によって変形しても、荷重を取り去れば元に戻る変形を弾性変形という。
荷重変形図では、弾性限界よりも左側で材料は弾性変形する。
弾性変形の例にスプリング式のバネがある。
適度な力でバネは伸びるが、力をなくなれば元にもどる。
力が過剰だと、バネが伸び切ってしまい元にもどらない。
これが塑性変形だ。
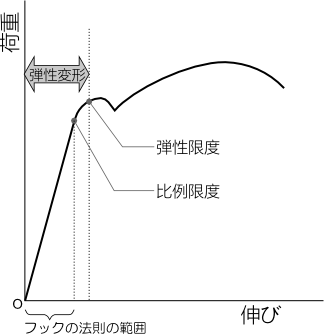
弾性変形には荷重と伸びが比例する範囲と、比例しない範囲がある。
その境界が比例限界だ。
材料によっては比例限界と弾性限界が近すぎて区別できない場合もある。
比例とは二つの量が一次関数で結びつくことをいう。
例えば、以下の式でaを比例定数とした場合、xとyは比例する。
\[
y=ax
\]
xが2倍になれば、yも2倍だ。
比例限界内であれば、荷重と伸びが比例する。
2倍伸ばしたければ、荷重を2倍にすればいい。
ここでは、荷重変形図を例にしたが、応力ひずみ曲線でも応力とひずみは比例する。
応力とひずみの比例関係を発見者の名をとってフックの法則という。
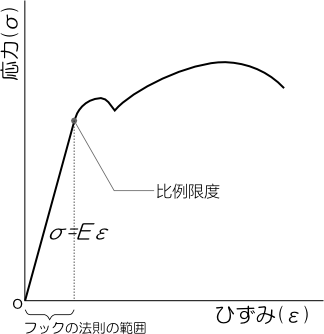
フックの法則での比例定数を弾性定数といいEで表す。
\[
\sigma=E\varepsilon
\]
比例限度から弾性限度の範囲では、荷重が増えると材料は伸びるものの、荷重と伸びは一次関数で結ばれていない。
グラフにしても直線にならないのだ。
スポンサーリンク
2016/12/23