ケプラーの法則
ケプラーの法則
ヨハネス・ケプラーによって発見された惑星の運動に関する法則をケプラーの法則という。
ケプラーの法則は、以下の3つの法則から構成されるため、ケプラーの3法則という場合もある。
| 第1法則 | 惑星の軌道はすべて楕円であり、太陽はその焦点である。 実は、天体の軌道はすべて円錐曲線になることの一面を表している |
| 第2法則 面積速度一定の法則 | 惑星と太陽を結ぶ直線が一定時間に作る面積は、惑星の居場所に無関係に一定である。 実は、角運動量保存の法則の一面を表している |
| 第3法則 | 惑星の公転周期の2乗は、軌道の半長径の3乗に比例する。 実は、万有引力の法則の一面を表している |
ケプラーは、太陽と惑星の間の法則としてケプラーの法則を発見した。
しかし、このケプラーの法則は、「太陽と惑星」だけでなく、「惑星と衛星」や「太陽系外の天体」にも適合する法則なのである。
ケプラーの第一法則
「惑星の軌道はすべて楕円である」というのは、分かりやすい。
惑星は、真円を描いて公転しているように思えるが、実は楕円軌道なのだ。
太陽はこの楕円軌道の中心ではなく焦点にいるのである。
ここで、楕円の焦点について解説しておこう。
定点からの距離が一定である点の集合を「円」という。
定点が「円の中心」、定点からの一定の距離が「半径」である。
これに対し、二つの定点F1, F2からの距離の和が一定である点の集合が「楕円」である。
この二つの定点F1, F2を「焦点」とよぶ。
下図の場合、楕円の円周上の点Pと焦点F1, F2とを結ぶ直線L1,L2の長さの和は、点Pの場所に依存せず常に一定となる。
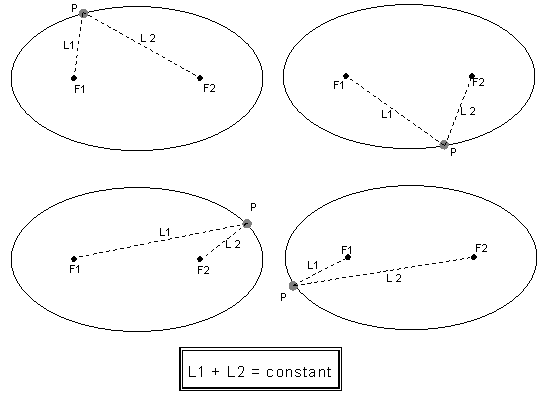
上記の定義から明らかなように、一つの楕円には、焦点が二つあることになる。
太陽は、その二つのうちの一つに位置しているというわけだ。
他方の焦点には、何もない。

ケプラーの第二法則
「惑星の軌道は楕円である」ということは、惑星と太陽の距離は、軌道上の場所によって少しづつ違うということを意味する。
惑星は楕円軌道を進むにつれ、太陽に近づいたり遠ざかったりするのだ。
軌道上で最も太陽に近い場所を「近日点」、最も遠い場所を「遠日点」という。
惑星が公転するスピードは場所によって異なる。
惑星は遠日点付近では、ゆっくりと進む。
反対に、近日点付近では、足早に通りすぎるように速く進んでいく。
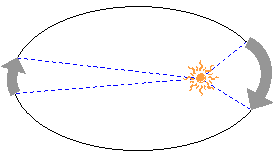
惑星と太陽を結ぶ直線を考えてみよう。
この直線は惑星の公転に従って扇型を形作ることになる。
惑星が一定時間に作り出す扇型の面積は、惑星が軌道上のどこにいても常に一定なのだ。
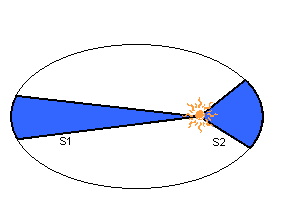
このことは、惑星は近日点付近ではスピードアップし、遠日点付近ではスローダウンすることを意味している。
一定時間に作る面積が、一定であることから、ケプラーの第二法則を特に「面積速度一定の法則」と呼ぶこともある。
ケプラーの第三法則
楕円形の二つの焦点を含み、円周に切り取られた線分を長軸という。
長軸の長さが長径、長径の半分が半長径だ。
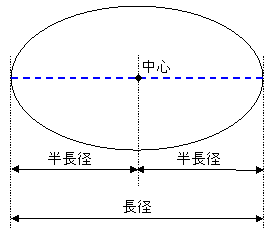
「惑星の公転周期の2乗と半長径の3乗の比は、すべての惑星で同一である」
これが、ケプラーの第三法則だ。
惑星の平均の軌道半径は、半長径で示す。
太陽からの距離を測っているのではないのだ。
「半長径の3乗」を「軌道半径の3乗」と表現している本もある。
両者は同じ意味だ。
■最初のページ:ピンポイント解説:目次
スポンサーリンク
2006/09/03