楕円

HOME＞ ピンポイント解説＞楕円＞楕円の性質

楕円の性質

楕円とは

円をつぶしたような形が楕円である。
つぶれ方の度合いにより、無数の楕円が存在する。

円を斜めから見た形といってもいいが、遠近の視覚のため完全な楕円にはならない。

楕円は「二つの定点からの距離の和が一定なとなる点の軌跡」と定義される。
定義の意味は、このページの後半の焦点で解説する。

長軸と短軸

真円なら半径は一定だが、楕円の半径は楕円上の場所によって違っている。
最も長い半径が長半径、最も短い半径が短半径だ。
以下の図ではaが長半径、bが短半径である。

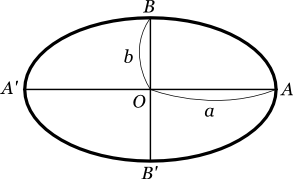
また、長半径となる軸を長軸、短半径となる軸を短軸という。
上記の図では長軸がAA'、短軸がBB'である。

焦点

長軸上に点Fと点F'を置き、楕円上の点Bから線分BFと線分BF'を引く。
このとき、線分BFと線分BF'の長さが、長半径aと等しくなるなら点Fおよび点F'を焦点という。

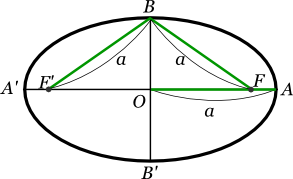
今度は楕円上の任意の点Pから二つの焦点に向けて、線分PFと線分PF'を引く。
すると、線分PFと線分PF'の長さの和は、2a(長半径の二倍)に等しくなる。
点Pが楕円上のどこにあっても、線分PFと線分PF'の長さの和は常に一定で、長半径の二倍に等しいのである。

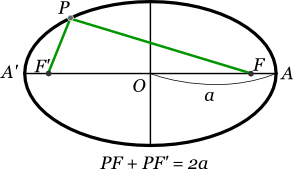
この焦点の性質を利用することで、楕円の定義は次のようになる。

楕円の定義：二つの定点からの距離の和が一定なとなる点の軌跡
二つの定点とは焦点のことだ。

離心率

焦点には、もう一つ重要な性質がある。

楕円上の任意の点Pから準線Lに垂線PHを引くと、PFとPHの比率は、点Pが楕円上のどこにあっても一定になる。
PFとPHの比率を離心率といいeで示す。

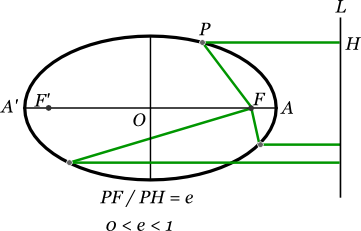
離心率は長半径aと、中心から焦点までの距離fの比率とも一致する。

上図から明らかなように、離心率は0より大きく、1よりも小さい。
真円は焦点が中心と一致しているため、真円の離心率は0となる。

■最初のページ：ピンポイント解説：目次

このページのTOPへ