熱力学の第一法則
熱力学の第一法則
仕事や熱が系(気体が充満しているシリンダ)に出入りすると、系の内部エネルギーが変化する。
内部エネルギーの変化は、状態量(温度、圧力、体積)の変化となって現れる。
(「状態量と状態方程式」参照)
上記の「仕事の出入り」とは、ピストンを押したり引いたりすることである。
「熱の出入り」とは、シリンダを暖めたり冷やしたりすることである。
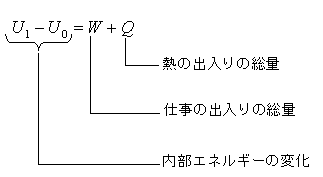
内部エネルギーがU0のシリンダに対し、仕事Wや熱Qが出入りした結果、内部エネルギーがU1に変化したとする。
このとき、仕事の出入り、熱出入りと内部エネルギーには、以下の関係がある。
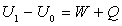
この式は「仕事Wや熱Qの出入りの総量は、内部エネルギーの変化に等しい」ということを表現している。
これを熱力学の第一法則という。
上記は、仕事Wや熱Qの出入りの総量についての議論だ。
これに対し、微小な仕事、微小な熱の出入りと、内部エネルギーの変化の関係は以下の式となる。
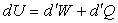
「dU」が「内部エネルギーの変化」を示すのは分かるとして、気になるのは「d'W」「d'Q」だ。
なぜ、「dW」「dQ」ではなく、ダッシュが付くのであろうか?
「状態量と状態方程式」で解説したように、仕事と熱は状態量ではない。
仕事や熱は状態量ではないので、「微小な変化」という発想はない。
ここで表現したいのは、「仕事の微小な変化」ではなく「微小な仕事の量」なのだ。
「微小な変化」と「微小な量」は本質的に違うものだ。
「微小な変化」であれば「d」で記述するが、それと異なる「微小な量」を同様に「d」で表現することはできない。
このため、仕事と熱には「d'」を用いるのだ。
なお、「d'」ではなく「δ」を用いて、熱力学の第一法則を解説している文献もある。
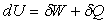
「δ」であっても同様に解釈すればいい。
熱力学の第一法則によれば、与えられた仕事や熱は内部エネルギーとなって系内に保有される。
系外に仕事や熱を提供すれば、それと等しい量の内部エネルギーが減少する。
ということは、熱力学の第一法則はエネルギー保存の法則の一部分を示していることになる。
以下の図が、この関係のイメージだ。
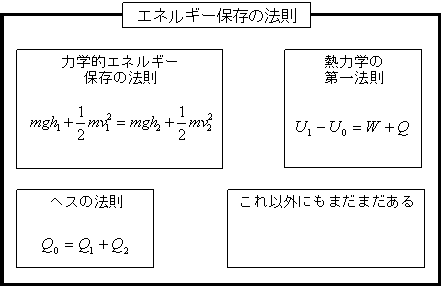
エネルギー保存の法則は、あらゆる状況で成り立つ自然界の根本の法則だ。
「力学的エネルギー保存の法則」や「熱力学の第一法則」「ヘスの法則」はその一部分にすぎない。
そして、根本の法則であるために、場面ごとに違った法則となって現れてくる。
物体が保存力のみを受けて運動すれば、力学的エネルギー保存の法則として現れる。
シリンダをピストンで押せば、熱力学の第一法則が現れる。
化学反応時の熱を観察すれば、ヘスの法則となって現れるのだ。
くれぐれも、「"力学的エネルギー保存の法則"と"熱力学の第一法則"を合わせたものが"エネルギー保存の法則"である」と誤解のないようにお願いする。
「第一法則」と言うからには、熱力学には「第ニ法則」もある。
「第ニ法則」はエントロピー増大の法則である。
「第三法則」はないが、時として、絶対零度よりもさらに低い温度はありえないことを、「熱力学の第3法則」という場合もある。
■次のページ:ブラウン運動
スポンサーリンク
2006/09/13