平均情報量
平均情報量
平均情報量とは
情報量は、事象が起こった結果に関する概念である。
これに対し、平均情報量は事象が起こる可能性についての概念である。
事象を起こす源を「情報源」という。
例えば、サイコロやコインを投げるといった行為は情報源である。
この情報源から「1の目が出た」「表が出た」といった情報が生じるのだ。
サイコロを投げて、各目が出る確率と、実際にその目が出たときの情報量を調べてみよう。
(計算方法は情報量参照)
| サイコロの目 | その目が出る確率 | その目が出たときの情報量 |
| 1 | 1/6 | 2.585 |
| 2 | 1/6 | 2.585 |
| 3 | 1/6 | 2.585 |
| 4 | 1/6 | 2.585 |
| 5 | 1/6 | 2.585 |
| 6 | 1/6 | 2.585 |
どの目も、出現する確率は同等に1/6で、情報量は2.585である。
つまり、サイコロを投げるという情報源では、平均して2.585 bitの情報量が生じることが分かる。
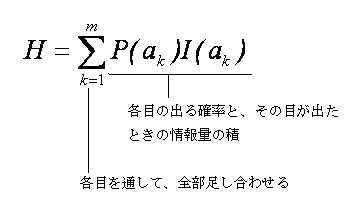
ある情報源から生じる情報量の平均を「平均情報量」といい、Hで表現する。
上記の例の場合は、H =2.585bitとなる。
この例の場合は、各目の出る確率も、そのときの情報量もすべて同一なので、直感で「H =2.585」と認識できる。
論理に立ち返れば、次のロジックで算出するのが本来だ。

これを、もっともらしく書くとこうなる。
情報源によっては、すべての事象が同一の確率で生じるとは限らない。
例えば、イカサマのサイコロがこれにあたる。
「1」が特に出やすく作られたサイコロを考えてみよう。
| サイコロの目 | その目が出る確率 | その目が出たときの情報量 |
| 1 | 5/10 | 1.000 |
| 2 | 1/10 | 3.322 |
| 3 | 1/10 | 3.322 |
| 4 | 1/10 | 3.322 |
| 5 | 1/10 | 3.322 |
| 6 | 1/10 | 3.322 |
この場合の平均情報量Hは、
(5/10) × 1.000 + 5×(1/10)×3.322=2.161 bit
となる。
もちろん、各目の発生確率が変化すれば、平均情報量Hも変わってくる。
極端な例として、「1」しか出ないサイコロの平均情報量Hは0 bitである。
1しか出ないサイコロを振って、1が出たところで何の意外性もないからだ。
| サイコロの目 | その目が出る確率 | その目が出たときの情報量 |
| 1 | 10/10 | 0.000 |
| 2 | 0/10 | -(log0は定義できない) |
| 3 | 0/10 | - |
| 4 | 0/10 | - |
| 5 | 0/10 | - |
| 6 | 0/10 | - |
ここまで、登場した3つのサイコロの平均情報量Hを比較してみよう。
| まともなサイコロ | イカサマのサイコロ | 「1」しか出ないサイコロ |
| 2.585 | 2.161 | 0 |
ここから分かるように、すべての事象が同一の確率で生じる場合、平均情報量Hが最大になる。
また、各事象の発生確率の偏りが大きいほど、平均情報量Hは小さくなる。
平均情報量とエントロピー
平均情報量は、エントロピー(entropy)ともいう。
エントロピーは、熱力学で登場する「乱雑さ」の指標でもある。
熱力学では「自然現象は乱雑さが増加する方向へ進行し、エントロピーは増大する」などと表現する。
乱雑なほどエントロピーは大きい。
「1」しか出ないサイコロよりも、まともなサイコロのほうが、より乱雑である。
出る目がまともに予測できないからだ。
英文はアルファベット26文字と空白のスペースから構成されるので、英文の平均情報量の最大値はlog 27=4.755 bitとなる。
これは、文字と空白スペースがまったくのランダムに並んだ場合だ。
実際の英文は、文字ごとの使用頻度の違い(Eが最も出現する)や、「Qの直後はUになる」等の法則がある。
このため、各文字の出現頻度が偏るため、現実の英文の平均情報量は、4.755 bitよりもはるかに低くなる。
■次のページ:マルコフ情報源
スポンサーリンク
2006/07/01