加法定理

HOME＞ ピンポイント解説＞加法定理(三角関数)

加法定理の導出

図による加法定理の導出

加法定理は角度を合成したときの三角関数の関係を示した定理である。
sin(α+β) = sin α cos β + cos α sin β
cos(α+β) = cos α cos β - sin α sin β

図を使って加法定理を導き出す手順を理解しておくと、公式を覚えやすい。
ここでは直角三角形を利用して加法定理の導出方法を説明する。

直角三角形を使った加法定理の導出方法

直角三角形△abcを用意する。
辺acの長さが1、内角がαなら、辺abはcos α、辺acはsin αとなる。

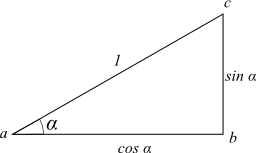
直角三角形△abcを、角度βだけ回転させると次の図になる。

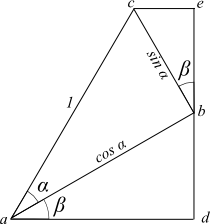
このとき、辺adの長さはcos α × cos βとなる。
なぜなら、cos β はad/ab、abはcos α だから代入すればいい。

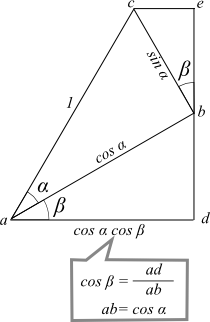
同様に各辺の長さは以下の図のようになる。

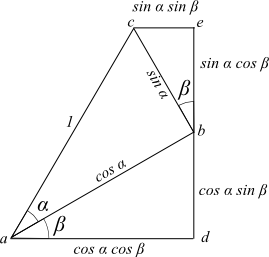
点cからadに垂線を引き、交点をfとする。
新たにできた直角三角形△afcの辺afは、cos(α+β)、辺cfはsin(α+β)となる。

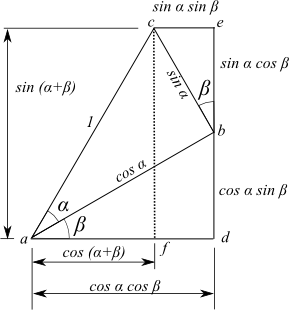
この図から次のことが見てわかる。
sin(α+β)は、sin α cos β と sin β cos αの和
cos(α+β)は、cos α cos β と sin α sin βの差

これを式で表現すると以下のように加法定理の公式になる。
sin(α+β) = sin α cos β + cos α sin β
cos(α+β) = cos α cos β - sin α sin β

このように図で導出方法を理解しておくと、加法定理の公式は忘れにくい。

次のページでは加法定理の公式のゴロ合わせによる暗記法を紹介する。

■次のページ：加法定理のゴロ合わせ暗記法

このページのTOPへ