ガウスの法則

HOME＞ 電磁気学＞ガウスの法則

ガウスの法則とは

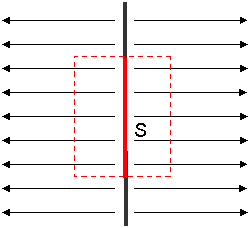
電気力線とガウスの法則

電気力線の本数と電荷量の関係をまとめたものがガウスの法則だ。
まず、ガウスの法則を示そう。
「任意の閉曲面を貫く電気力線の総本数は、その閉曲面内の電荷の総和を誘電率で割ったものに等しい」

「任意の閉曲面」なのでどんな閉曲面でもいい。
この閉曲面の内部の電荷qから放射され、閉曲面の表面を貫く電気力線の本数はつねに
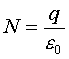となるのだ。

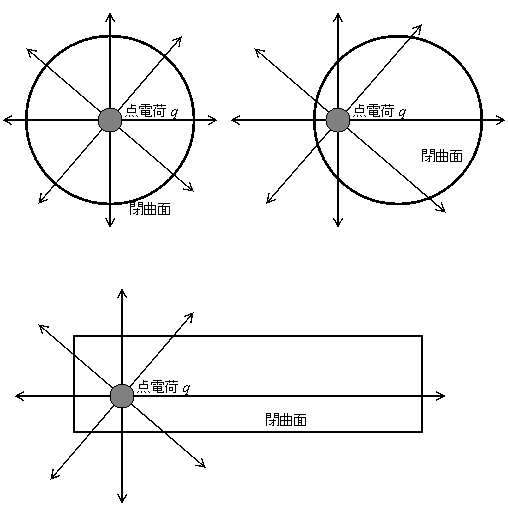
次の図の例では、点電荷から８本の電気力線が放射されている。

この点電荷を閉曲面で囲んでみよう。
閉曲面を貫く電気力線はすべて８本である。
点電荷の位置は閉曲面の中心であっても、中心から外れていてもかまわない。
球状でなくてもいいのである。
閉曲面があってもなくても点電荷qから放射される電気力線の本数は変化がないからだ。

さらに複雑な形状の閉曲面で囲んでみよう。
以下の例の場合、一度閉曲面から出た電気力線が再度、閉曲面に進入している。
この閉曲面から出る電気力線は延べ10本、入る電気力線は延べ12本である。
10-2=8で差し引き8本の電気力線が閉局面から出ることになる。

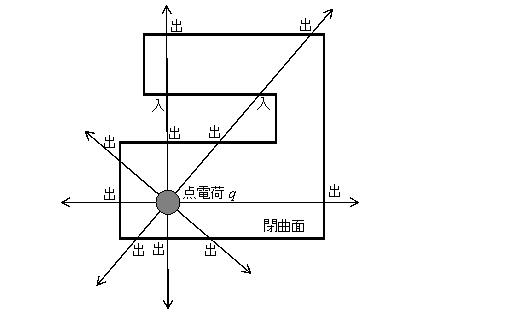
どんな複雑な形状の閉曲面で囲もうが、その閉曲面を貫く電気力線の本数はいつも同じになるということだ。
そして、ガウスの法則では電気力線の本数は「電荷の総和を誘電率で割ったもの」に等しくなる。

ガウスの定理

Q[C]の電荷からはQ/ε[本]の電気力線が放射される。
単独の電荷がQ[C]であっても、複数の電荷の合計がQ[C]であっても同じだ。
放射される電気力線の総本数がQ/ε[本]になるのである。

この電荷を閉曲面で囲めば、上図のようになる。
電荷を閉曲面で囲んだ様子を言い表した表現がガウスの定理だ。

ガウスの定理は
任意の閉曲面を通過する電気力線の本数は、閉曲面内部にある電荷の総和の1/εになる。
となる。

閉曲面を通過する電気力線の総本数はQ/ε[本]だ。
この総本数Q/εを閉曲面の総面積Sで割った値は、「単位面積あたりの電気力線の本数E」になる。
元々、単位面積を通過する電気力線の本数は、その場の電場の強さに等しいとして定義した。
ということは、「電荷Q」と「電荷を囲む閉曲面の総面積S」が分かれば、ガウスの定理を利用して電場の強さEを求めることができるのだ。

ここで、ガウスの定理を数式で確認してみよう。

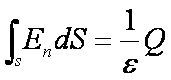
右辺は、電荷Qを誘電率εで割っているので、閉曲面を通過する電気力線の総本数を表している。
左辺は、単位面積を通過する電気力線の本数(=電場の強さ)を、閉曲面の全面積で積分したものだ。
これは電気力線の総本数に相当する。
つまり、右辺も左辺も閉曲面を貫く電気力線の本数を意味することになる。

点電荷が作る電場の強さはクーロンの法則によって求める。 ところが、電荷が面状に分布している場合ではクーロンの法則は使いにくい。 「電場の強さを求めよ」という設問中に「面状に分布した電荷」が登場すれば、ガウスの定理を活用するのがセオリーだ。

電場の強度は、
点電荷の場合はクーロンの法則
面状に分布しているときはガウスの定理
を用いて計算する。

■最初のページ：電磁気学：目次

このページのTOPへ