電気力線
電気力線の数
クーロンの法則の式を再度示そう。
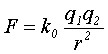
つまり、「2つの電荷が及ぼしあう力は、電荷の積に比例し距離に反比例する」ということだ。
このときの比例定数k0の値は「9×10」である。
さて、この比例定数k0を以下のように定義してみよう。
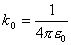
新たにε0と円周率πが加わった。
ε0を真空の誘電率という。
このような定義をしていったい何の得があるのだろうか?
繰り返しになるが「単位面積あたりの電気力線の本数(電気力線密度)はその場所の電場の強さに等しい」と決めた。
「決めた」のだ。
電気力線を観測しその本数を数えたら、「電場の強さと同じでした」というのではない。
電気力線は実在しないからだ。
「本当は存在しないけれど、存在するとして考えましょう。他の物理現象の検討がとっても楽になりますよ」といったものだ。
真空中に存在するプラスの点電荷qを考えよう。
点電荷qからは電気力線が放射されている。
その電気力線の本数をNとする。
点電荷qから距離rだけ離れた場所の電界の強さEは
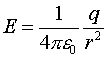
となる。
「単位面積あたりの電気力線の本数」(電気力線密度)は、その場所での電場Eの値と一致すると決めた。
ここで点電荷を中心とする半径rの球の表面積Sを考えると
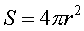 となる。
となる。
「単位面積あたりの電気力線の本数」に「表面積S」をかけると電気力線の全部の本数になる。
これは、電荷から放射される電気力線の本数Nと同じだ。
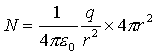
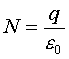
つまり点電荷qから放射される電気力線の本数は、電荷量を誘電率で割ったものに等しいというわけだ。
ここではプラスの電荷を考えたが、マイナスの電荷であっても同様だ。
マイナス電荷の場合は「吸収される電気力線の本数は、電荷量を誘電率で割ったものに等しい」となる。
真空の誘電率を定義することによって、電気力線の本数と電荷が簡潔に関連付けられるのである。
真空中に限らず、他の物質中でも同様である。
この考え方がガウスの法則の基本となる。
■最初のページ:電磁気学:目次
スポンサーリンク
2005/06/18