荷重変形図
荷重変形図の各部の名前
前ページで書いたように、荷重変形図の各場所にはそれぞれ名前がある。
(下図参照)
ここでは、これらを詳しく解説する。
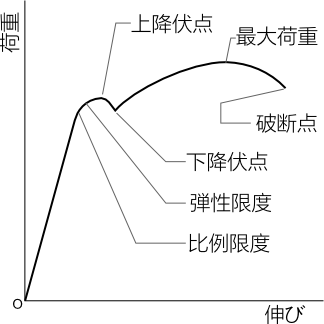
比例限度
原点Oから比例限度の範囲では、与えた荷重と試験片の変形量とは完全に比例する。
比例関係であるので、荷重が2倍になれば変形量も2倍だ。
材料をさらに伸ばすには、さらに荷重が必要なのだ。
荷重を取り去れば、試験片の形も完全に元に戻る。
比例限度を超えると、荷重と試験片の変形量は比例しなくなる。
弾性限度
比例限度を超えると荷重と試験片の変形量は比例しなくなるものの、荷重を取り去れば試験片完全に元の形に戻るという性質に変わりはない。
このように荷重により変形しても、荷重がゼロになれば、元に戻るような変形を弾性変形という。
しかし、弾性変形が維持されるのも弾性限度までだ。
弾性限度を超えると、荷重をゼロにしても変形が残ってしまう。
比例限度と弾性限度は、ほぼ同じ値になる場合が多い。
上降伏点
弾性限度を超えると、荷重をゼロにしても材料は元の形に戻ることはない。
このような変形を塑性変形という。
降伏点に至るまでの範囲では、試験片をさらに伸ばしたければ、荷重をさらに増加させる必要がある。
ところが上降伏点を超えると、試験片をさらに伸ばすのに、さらに強い荷重は必要がなくなるのだ。
荷重を増加させなくても(荷重を少し低くしても)、材料を伸ばすことが可能だ。
荷重変形図で上降伏点を過ぎた部分の線が右に下がっているのはこのためである。
下降伏点
荷重変形図のカーブが再び上昇に転じるのが下降伏点だ。
ここを過ぎると、試験片をさらに伸ばすなら、荷重をさらに増加させる必要がある。
上降伏点と下降伏点を合わせて単に降伏点と呼ぶ。
JISでは上降伏点を降伏点としている。
極限強さ
を極限強さとはグラフが最も高くなる点である。
この長さまで伸びたときに、最も大きな荷重が必要である。
破断点
極限強さを超えると、試験片はくびれて細くなる。
やがて伸びて破断する。ここを破断点という。
■最初のページ:材料力学:目次
スポンサーリンク
2016/12/20