等加速度直線運動

HOME＞ 質点の力学＞等加速度直線運動＞等加速度直線運動とは

等加速度直線運動の公式

v-tグラフと等加速度直線運動

同じ速度を保ったまま直進する運動を、等速直線運動という。
これに対し、一定の割合で速度が上昇していく直進運動が、等加速度直線運動だ。
v-tグラフで比較すると等速直線運動は水平だが、等加速度直線運動は斜めになる。

単位時間あたり(1秒あたり)の速度の変化を加速度といい、通常はaで示す。
v-tグラフの傾きが加速度\(a\) に相当する。

等速直線運動は一定速度のため速度は変化しない。つまり加速度はゼロだ。
このため、v-tグラフは水平になる(傾きがゼロになる)。

速度×時間＝移動距離の関係がある。
v-tグラフの縦軸は速度、横軸は時間だ。
ということは、縦軸(速度)×横軸(時間)で示される面積が移動距離を表していることになる。

ここまでの内容を用いれば、簡単に等加速度直線運動の3つの式を導きだすことができる。
順を追って説明しよう。

速度の式

等加速度直線運動の速度は以下の式で表現する。 \[ v=v_{ 0 }+at \]

加速度\(a\)は1秒あたりの速度の増加分である。
2秒後に速度は\(2a\)だけ増え、 10秒後に速度は\(10a\) だけ増える。
だから\(t\) 後の速度は\(at\) となる。
加速度\(a\) はこのグラフの傾きになるのだ。

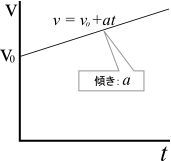
速度ゼロから加速したなら上記でいいが、実際には初速度\(v_{ 0 }\) を持つケースが多い。

等加速度直線運動は初速度\(v_{ 0 }\) から徐々に加速度\(a\)でスピードアップしていくのだ。
だから、初速度\(v_{ 0 }\) に\(at\) を加えた式が、等加速度直線運動の速度の式となる。
\[ v=v_{ 0 }+at \]

移動距離の式

等加速度直線運動の移動距離は以下の式で表現する。
\[ s=v_{ 0 }t+\frac{ 1 }{ 2 }at^2 \]

移動距離はv-tグラフの面積であった。
等加速度直線運動の移動距離は、v-tグラフを上下二つに分けて計算する。

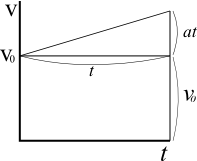
下側の面積は簡単だ。
縦×横が面積なので、初速度\(v_{ 0 }\) と経過時間\(t\) の積を求めればいい。

上側の三角形の領域は、底辺×高さ÷2(三角形の面積)の公式を適用する。
底辺は\(t\) だ。

加速度\(a\)は1秒後に速度\(a\)となり、2秒後に速度\(2a\)、 t秒後に速度\(at\)となる。
速度は縦軸だから三角形の領域の高さに相当する。

底辺(\(t\) )と高さ(\(at\) )の積に\(\frac{ 1 }{ 2 }\) をかけた値が上部の三角形の面積だ。
これを下側の面積と合わせれば、以下の式となり全体の面積を表すことになる。
\[ s=v_{ 0 }t+\frac{ 1 }{ 2 }at^2 \]

速度と移動距離の関係式

速度の式と移動距離の式から\(t\)を消去すると、以下の式が得られる。
\[ v^2-v_{ 0 }^2=2a(x-x_{ 0 }) \]

移動距離とは位置の変化のことだ。
位置が\(x_{ 0 }\)から\(x\)に移動したとすれば、\(s=x-x_{ 0 }\)である。
これを代入すると以下の式が得られる。
\[ v^2-v_{ 0 }^2=2as \]

エネルギーの原理の式を導出するとき、この式が出発点となる。

■最初のページ：質点の力学：目次

このページのTOPへ