万有引力の法則

HOME＞ 質点の力学＞万有引力の法則＞万有引力の法則とは

万有引力の法則の証明

加速度による証明

万有引力の法則の正しさは、月の観測によって証明された。

月は地球を中心として円運動している。
円運動であるので中心に向う加速度を生じているはずである。
ニュートンの時代、月までの距離(約38万km)や月の公転周期(約27.32日＝2360448秒)、地球の半径(約6370km)はすでに確認されていた。

これらの値を使用して月の加速度を求めてみよう。
円運動の加速度の式を以下に示す。
Rは月まで距離、vは公転の早さ、つまり公転軌道の距離(Ｒを2π倍したもの)を公転周期で割ったものだ。


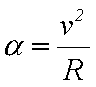
これに具体的に数値を代入してみると

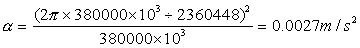
このようにして求めることができた。
ここで注目して欲しいのは、上記の加速度は万有引力の法則を使用せずに月の加速度を求めたということだ。

次に万有引力の法則を使用して月の加速度を求めてみよう。
万有引力の式

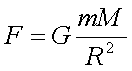
が正しいのなら、この式から導出される月の加速度も約0.0027m/s²となるはずだ。
地球の引力の影響を受けた物体には、重力加速度が生じる。
その値は質量の大小には無関係に一定で約9.78m/s²である。

地球の引力は月にも及び、月を地球に向って引きつけようとする加速度αmを生じているはずである。
月までの距離は地球の半径の60倍なので、加速度αmは地表付近での重力加速度の1/60²に相当する。(万有引力は距離の２乗に反比例すると仮定したので)
これを計算すると

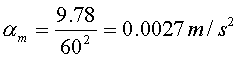
となる。
つまり重力加速度と加速度αmは一致するので万有引力は正しいと判断できる。

ケプラーの第三法則と万有引力の法則の関係を次のページで解説する。

■次のページ：ケプラーの第三法則と万有引力の法則

このページのTOPへ