仕事
力に抗しての仕事
「仕事をする」と言っても、これには次の２系統ある。
「力が仕事する」場合
「力に抗して仕事をする」場合
この２系統の区別は紛らわしい。
重力を例にして解説しよう。
| 力が仕事する | 力に抗して仕事をする |
| 高さhにある質量mの物体が、自然落下し地面に衝突したとする。 このとき、重力がこの物体にした仕事はmghである。 |
地面にある物体を、重力と等大逆向きの力でゆっくり高さhまで持ち上げたとする。 このとき手が重力に抗してした仕事はmghである。 |
「力が仕事する」に関しては問題ないであろう。
仕事の定義そのものだからだ。
一方で、「力に抗して仕事をする」はしっくりこない。
違和感を覚えるポイントは以下の二つだ。
・重力と等大逆向きであれば合力はゼロになるので、仕事にならないのではないか？
・なぜ「ゆっくり」持ち上げるのか？
手のひらの上で、物体が静止している場合、力は以下のように等大逆向きとなる。
物体はmgの力で手のひらを押す
手のひらは上向きの力mgで物体を押す
二つの力の合力は、ゼロだ。
ここで微少な力⊿Fの分だけ余計に力を加えれば、物体を上に向って動かすことができる。
高さhまでの過程の前半は、mg＋⊿Fで持ち上げ、後半はmg－⊿Fで持ち上げる。
そうすると、力がした仕事は
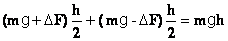
となる。
⊿Fが非常に小さければ、物体にかかる加速度a=⊿F /mも小さくなるので、持ち上げる操作に時間がかかる。
⊿F→0とすれば、全工程を通してmgの力で無限に遅い速度で持ち上げたのと同等になる。
この場合、持ち上げていくどの時点においても、持ち上げる力はmgである。
非常に「ゆっくり」とは、⊿Fを無限に小さくすることによってmgと等大逆向きの力を実現しようとする意図があるのだ。
上記では速度を前半、後半で分けた。
前半、後半と分離しないで、mg＋⊿Fの力で通して持ち上げてはいけないのだろうか？
この場合、高さhまで持ち上げる全過程で、a=⊿F /mの加速度がかかる。
そうすると、この物体は等加速度運動をするため、hに達した時点で速度を持つためhの位置にピタリと停止できない。
後述するが、高さhにある物体は、ポテンシャルエネルギーmghを持つ。
等大逆向きの力mgでhまで移動する仕事がポテンシャルエネルギーmghと一致するように定義したい。
もし、高さhに達した時点で速度を持っていればポテンシャルエネルギーmghに加えて、運動エネルギーも持つことになり具合が悪い。
運動エネルギーが生じないようにするためには、ｈでピタリと停止する必要がある。
そのために、速度はゆっくり持ち上げなくてはならないのだ。
前半、後半とで分離し⊿Fの符号を反転することにより、ｈでピタリと停止するのだ。
管理人の関連サイト
地学・天文学・固体地球・宇宙科学の基本の解説
祝日と祭日、シカとトナカイ、干支と十二支は何が違うのか？
2005/08/27
物理の基礎基本・試験対策・レポート対策 |
||
物理学解体新書・HOME |
||
|
|
||