情報科学

２進数→10進数の変換

10進数と２進数の変換は、方向によって方法が異なる。

方向	方法の概略
２進数→10進数の変換	位取り記数法を利用する。
10進数→２進数の変換	２で割って得た余りを利用する。

ここでは、２進数→10進数の変換方法を解説する。
(10進数→２進数の変換方法は次のページ参照)

数は0、1〜9までの十個の文字を使用して表現する。
(小数点や、３桁ごとの区切りのコンマは除く)

例えば「五百五」は「505」と記述する。
この場合、「百の位の5」と「一の位の5」では、同じ文字「5」を書いているのにその意味はまるで違う。
「百の位の5」は「一の位の5」に比べて、100倍の重みを持っているのだ。

つまり、数字は、桁の中の位置(百の位、一の位 等)によって、数の意味・重みが決まるのだ。
このような数字の表現方法を「位取り記数法」という。

位取り記数法の優位は、ローマ数字と比較するとよく分かる。

位取り記数法	ローマ数字
1	Ｉ
10	Ｘ
100	Ｃ
1000	Ｍ

ローマ数字は、数値が10倍になるごとに新たな文字を定義しなくてはならない。
しかし、位取り記数法では、10倍ごとに桁を一つ増やすだけでいい。
このため、どんなに巨大な数値を表現する場合でも十個の文字(0、1〜9)で、間に合うのだ。

「2345」という数値を、「桁の中の位置(位)ごとの意味・重みの違い」を意識して書くと次のようになる。

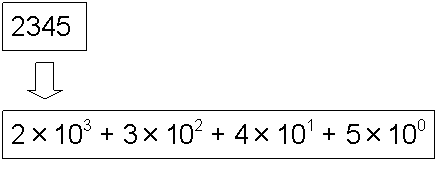
これを見ると、十の位とは「10¹の位」、百の位とは「10²の位」、千の位とは「10³の位」を示していることが確認できる。
位取り記数法では、10進数は10倍ごとに桁が一つずつ増えていくのだ。

なお、X⁰=1である。当然10⁰＝1である。

二進数の表記も、同様に位取り記数法を採用している。

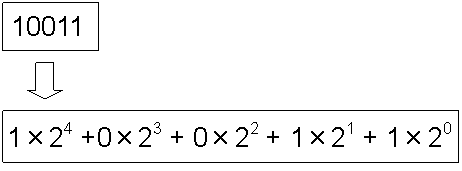
二進数の各桁は、「2⁰の位」、「2¹の位」、「2²の位」、「2³の位」・・・を示している。
10進数との違いは、2倍ごとに桁が一つずつ増えていくことにある。
ここで、各桁の位を整数に直して計算すれば、二進数から十進数に変換することができるのだ。

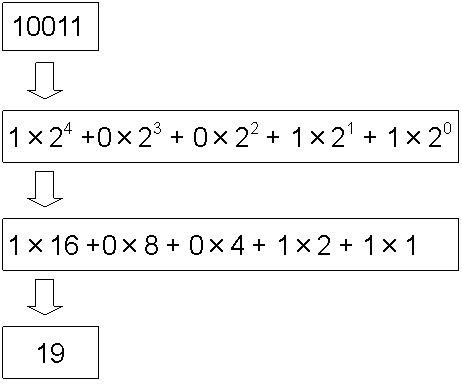
位取り記数法を利用すれば、５進数や８進数も10進数に変換することができる。
各桁の重みを5⁰、5¹、5²、5³・・・・、または8⁰、8¹、8²、8³・・・・とすればいい。

2006/07/01

前ページ	このページの先頭	次ページ
物理の基礎基本・試験対策・レポート対策
物理学解体新書・HOME