弧度法(ラジアン)
弧度法(ラジアン)の定義
単位円と弧度法(ラジアン)
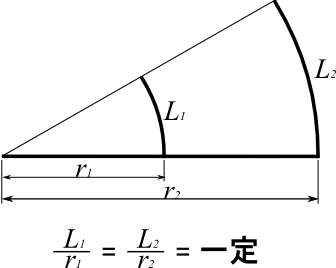
中心角が一定の場合、弧の長さと半径は比例関係になる。
直径が10倍になれば弧の長さも10倍になる。
直径がn倍ならば、弧の長さもn倍だ。
どんなサイズの扇型であってもこの関係は守られる。
弧の長さと半径は比は一定なのだ。
中心角が異なれば、弧の長さと半径の比は違ってくる。
中心角が2倍になれば、弧の長さと半径の比は2倍になる。
中心角が半分なら、弧の長さと半径の比も半分だ。
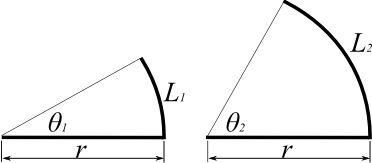
例えば、半径rの扇型を考えてみよう。
中心角が90度から180度と二倍になれば、弧の長さと半径の比も2倍になっている。
(下表)
| 中心角 | 90度 | 180度 |
| 半径 | r | r |
| 弧の長さ | πr/2 | πr |
| 弧の長さと半径の比 | π/2 | π |
上表を見ると、弧の長さと半径の比に半径rが含まれていないことに気がつく。
弧の長さと半径の比には、扇型のサイズは無関係なことを示している。
ここから、弧の長さと半径の比を使って中心角を表現するいう発想が生まれた。
これが弧度法だ。
■次のページ:弧度法:弧の長さと半径の比
スポンサーリンク
2010/02/14