円周率の求め方
多角形による円周率の近似
正多角形の角の数を増やしていくと、形が円に近付いていく。
次の図では、角の数を6から24に増やすだけで、かなり円に近付くことがわかる。
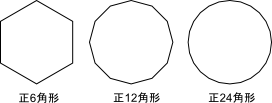
このとき、正多角形の辺の長さの合計値も、円周の長さに近づくことになる。
ここでは、正多角形の辺の長さの合計値から、円周の長さを近似で求めてみよう。
正多角形の角の数をn、一つの辺の長さをsとすると、正多角形の辺の長さの合計値Lはnsとなる。
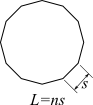
nが大きくなれば(正多角形の角の数が増えれば)、一辺が短くなるのでsは小さくなる。
その結果、Lが円周の長さに近づいていくのだ。
ここでは、n=3、つまり正三角形で考えてみよう。
半径rの円に正三角形abcを内接させる。
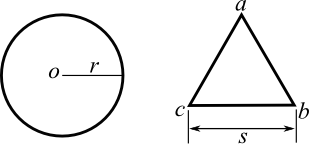
中心oと頂点bの線分obの距離は、半径と同じrだ。
oから線分cbに垂線を引き交点をdとすると、bdの大きさはsの半分になる。

この関係は表す式は次のようになる。
\[
\frac{ 1 }{ 2 }s=r\sin \theta
\]
\(\theta\)は、1周360度(2\(\pi\))を、角の数n(この場合はn=3)で割った値の、さらに半分だ。
従って\(\theta\)は次の式で表現することができる。
\[
\theta=\frac{ 1 }{ 2 }\frac{ 1 }{ n }2\pi
\]
これを代入すると、
\[
s=2r\sin \frac{ 1 }{ n }\pi
\]
となる。
正多角形の辺の長さの合計値Lは角の数nと一辺の長さsの積であった。
従って、Lは以下の式となる。
\[
L=2nr\sin \frac{ 1 }{ n }\pi
\]
一方、円の直径2rであるから、nが大きな値のとき、L/2rが円周率に近似されることになる。
\[
\frac{ L }{ 2r }=n\sin \frac{ 1 }{ n }\pi
\]
実際にnに数字を入れた結果が以下の表だ。
| 正n角形 | 円周率の近似値(L/2r) |
| 3 | 2.598076 |
| 4 | 2.828427 |
| 5 | 2.938926 |
| 6 | 3.000000 |
| 7 | 3.037186 |
| 8 | 3.061467 |
| 9 | 3.078181 |
| 10 | 3.090170 |
| 11 | 3.099058 |
| 12 | 3.105829 |
| 13 | 3.111104 |
| 14 | 3.115293 |
| 15 | 3.118675 |
| 16 | 3.121445 |
| 17 | 3.123742 |
| 18 | 3.125667 |
| 19 | 3.127297 |
| 20 | 3.128689 |
| 21 | 3.129888 |
| 22 | 3.130926 |
| 23 | 3.131833 |
| 24 | 3.132629 |
| 25 | 3.133331 |
角の数が増えるにつれ、より実際の円周率に近い値となっていく。
さらにnの数を増やした下表を見ると、正2000角形あたりから、小数点以下5桁まで近似されていることが分かる。
| 正n角形 | 円周率の近似値(L/2r) |
| 100 | 3.1410759 |
| 500 | 3.1415720 |
| 1000 | 3.1415875 |
| 2000 | 3.1415914 |
| 10000 | 3.1415926 |
■最初のページ:ピンポイント解説:目次
スポンサーリンク
2016/10/01