静電容量
静電容量とは
静電容量とは、導体が電荷を蓄える能力をいい、電位あたりの電荷で示す。
「容量」と言っても「これ以上電荷を蓄えたら、導体が壊れてしまいますよ」といった限界を示しているのではない。
半径aの球状の導体があり、その表面に電荷Qが一様に分布している。
この表面での電位はQ/4πε0aである。
もし、二倍の電荷が帯電していたら、電位は2Q/4πε0aである。
電荷が2倍なら電位も2倍、3倍なら3倍、つまり電荷Qと電位Vは比例関係にあるのだ。
比例定数は4πε0aであるが、これは球状の導体を検討したからであって、違う形状では、異なった比例定数となる。
形状ごとに比例定数が異なるのは面倒なので、比例定数をCとして代表しよう。
さきほどの電荷Qと電位Vの関係は以下の式で表現できる。
Q=CV
この比例定数Cを静電容量と呼ぶ。
この式から、以下の意味が読み取れる。
・静電容量Cが同じだったら、蓄えた電荷が大きいと電位も高くなる
・静電容量Cが大きければ、少ない電位でも大きな電荷が蓄えられる
帯電した導体に対し、さらに電荷を加えるためには仕事を要する。
導体上の電荷が作る電位に逆らって、電荷を運びこまなくてはならないからだ。
下図のように、電気力線の流れに逆行して電荷を運ぶイメージが理解しやすい。
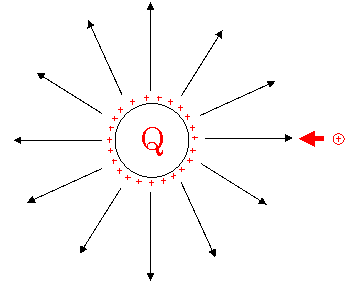
もし、導体の電位が小さければこの仕事は少なくて済む。
電気力線の本数が減るので、逆行が楽になるからだ。
このことから、静電容量が大きい方が、電位が低いので電荷がためやすいことが分かる。
導体により多くの電荷を蓄えたいのであれば、できるだけ大きな静電容量が必要になるのである。
ここで疑問が生じる。
導体のカタマリの静電容量と、コンデンサの静電容量の関連はどうなっているのであろうか?
コンデンサは二枚の平行板(極板)から構成される電気部品であり、カタマリではない。
同じ静電容量でありながら、両者は異質のように思える。
コンデンサは極板と極板の間に電荷が蓄えられるイメージがあるが、これは誤解だ。
実際には極板の表面に電荷が蓄積される。
極板も導体のカタマリであることに変わりない。
コンデンサの静電容量は、一方の極板(導体)の静電容量を指しているのだ。
帯電した板状の導体のカタマリ(A)に、さらに電荷を加えるためには仕事を要する。
これは球状の導体と同じ理由だ。
電気力線に逆行する必要があるからだ。
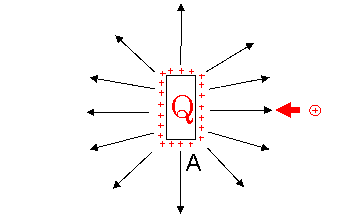
この導体Aに、もうひとつ導体Bを対面させる。
対面した導体Bは接地(アース)しておく。
静電誘導のため、導体BにはAに近い側にマイナス電荷が集まり、プラス電荷はアースを通して大地に逃げる。
導体AもBに近い側にプラス電荷が集まる。
その結果、電気力線は板の間に集中することになる。
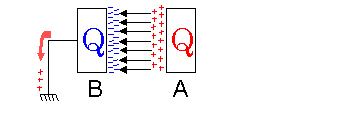
この状態で、さらに導体Aに電荷を加える場合、そのための仕事は少なくて済む。
電気力線に邪魔されることなく、悠々と電荷が運べるからだ。
当然、電荷は貯めやすくなる。
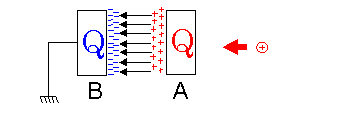
板の面積が大きいほど、板の間隔が狭いほど、この傾向は強くなり、ますます電荷が蓄積しやすくなる。
「電荷は貯めやすいこと」は「静電容量が大きいこと」とイコールだ。
板状の導体を極力狭く対向させ、面積を大きくすることは、導体の静電容量Cを大きくするテクニックなのだ。
これはコンデンサの基本構造に他ならない。
コンデンサは、電荷を蓄えると言うが本当は蓄えていない。
二枚の極板にはそれぞれ逆極性の電荷が蓄積されるので、コンデンサ全体で考えれば、電荷はゼロなのだ。
コンデンサは電荷を分離していると考えるのが本質なのだ。
電荷が蓄積している場所はコンデンサ全体ではなく、一方の極板である。
コンデンサの静電容量とは、一方の極板の静電容量のことなのだ。
ここを押えておけば、導体のカタマリとコンデンサの静電容量の違いに困惑することはないだろう。
■次のページ:静電エネルギー
スポンサーリンク
2005/06/18