電気力線

電気力線とは

電場の様子を目で見て理解できるように工夫したのが電気力線だ。
電気力線という実体がこの世に存在するのではない。
存在すると仮想すると他の物理現象を合理的に説明することができる。

電気力線は以下のように定義する。

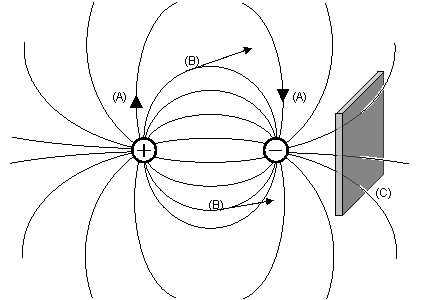
上記の定義により以下の性質が現れる。

電気力線は、物理現象を説明するために、存在すると仮定した線である。
電場があるところ、電気力線が通っていると仮定する。

電気力線の本数も仮定されている。
電場の強さがE[V/m]ならば、その場所を通る電気力線の本数は、単位面積あたりE本となる。
仮に10[V/m]の電場なら、この電場に垂直な平面を通過する電気力線は1[m ²]につき10本だ。

このように仮定すると、1つの電荷から放たれる電気力線の本数を数えることができるようになる。
真空中のQ[C]の電荷から、r[m]離れた場所の電場の強さEは次のようになる。

E=(1/4πε₀)(1/r²)Q

このEは電場の強さであると同時に、単位面積あたりの電気力線の本数ということを示している。
電荷を中心とする半径rの球の表面積Sを、このEにかければ、その値ESは球の表面を貫く電気力線の総本数になる。
つまり、電荷から放射された電気力線の総本数を示しているのである。

電荷を中心とする半径rの球の表面積Sは次の式で表現できる。
S=4πr²

このSとEの積を求めるのだから、
ES=(1/ε₀)Q
となる。

Q=1、つまり単位電荷の場合、真空中では1.13×10¹¹本の電気力線が放射されていることになる。

単位電荷から1.13×10¹¹本も放射されたのでは、計算もやりにくい。
しかもこの本数は物質によって異なった値になる。
誘電率εは物質毎に違うからだ。

電気力線の不便さを補うために電束という考えが導入された。
電束は電気力線の束(たば)である。

電束は1[C]の電荷からは1束、Q[C]の電荷からはQ束が放射される。
電荷から放射される束の数は、物質によらず、電荷量だけで決まるのだ。

真空中では、単位電荷から、1.13×10¹¹本の電気力線が放射された。
電束では、これが1束になる。
1.13×10¹¹本の電気力線を束ねたものが、電束なのだ。

Q[C]の電荷から、(1/ε₀)Q本の電気力線が放射されるが、同時にQ束の電束が放射されてると考えることもできる。
つまり、電気力線の本数をε倍すると、電束になるのだ。

単位面積あたりの電気力線の本数は電場の強さと同等なのでEで表せた。
このEをε倍すれば、単位面積あたりの電束になる。
(単位面積あたりの電束)＝ε×(単位面積あたりの電気力線の本数)

単位面積あたりの電束は電束密度といいＤで表現される。
ここから
D=εE
という関係が導き出せるのだ。

■次のページ：電気力線の数

2005/06/18
2008/01/09