ドップラー効果

HOME＞波動＞ドップラー効果＞ドップラー効果とは

音源が動く場合のドップラー効果

ドップラー効果の公式の導出

音源が動く場合のドップラー効果の例は、救急車のサイレン音だ。
救急車が接近してくるときは高く、離れていくときは低く聞こえる。
ここでは、音源が動く場合のドップラー効果の公式の導出を解説する。

静止している音源から周波数\(\nu_{ S }\)の音が出ているとする。
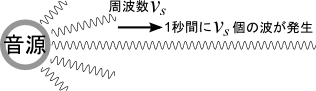
周波数は一秒間に繰り返す波の数だ。
だから、周波数が\(\nu_{ S }\)なら、一秒間に\(\nu_{ S }\)個の波が音源から生み出されていることになる。

A地点で静止している観測者が音源の音を聞いている。
音源も観測者も静止しているから、ドップラー効果は生じない。
だから、観測者の耳に入る周波数\(\nu_{ O }\)は音源の周波数\(\nu_{ S }\)と等しい。

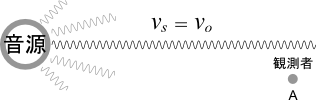
音速を\(V\)とすると、音源で発生した音は、一秒間に\(V\)メートル進むことになる。
速度は一秒間で進む距離だからだ。

ここで音源が\(v_{ S }\)の速度で、観測者に向かって動き出す。
この音源は、1秒間に\(v_{ S }\)メートル進むことになる。

1秒間で音が\(V\)メートル進み、音源が音の後を追って\(v_{ S }\)メートル進んだ。
つまり、一秒後に\(V-v_{ S }\)の距離の間に\(\nu_{ S }\)個の波が等間隔で並んだことになる。
波の個数を距離で割れば、1メートルあたり \(\displaystyle \frac{ \nu_{ S } }{ V-v_{ S } }\)個の波があることが分かる。

一方、音波は観測者のいる場所を音速\(V\)で通過する。
通過していく音波は1秒あたり\(V\)メートルだ。

\(V\)メートルと、1メートルあたりの波の個数\(\displaystyle \frac{ \nu_{ S } }{ V-v_{ S } }\)の積は、1秒あたりに通過する波の個数になる。
つまり 1秒間に\(\displaystyle \frac{ \nu_{ S } }{ V-v_{ S } }\times V\)個の波が観測者の耳に入るのだ。

1秒間の波の数が周波数である。
したがって聞く人の耳に入る音の周波数\(\nu_{ O }\)は次式となる。
\[ \nu_{ O }=\displaystyle \nu_{ S }\frac{ V }{ V-v_{ S } } \]

上式は音源が観測者近づく場合だが、音源が遠ざかる場合は、移動速度をマイナスにすればいい。
方向が逆だから符号も反対になるのである。
\[ \nu_{ O }=\displaystyle \nu_{ S }\frac{ V }{ V+v_{ S } } \]

■最初のページ：波動：目次

このページのTOPへ