ネイピア数

HOME＞ ピンポイント解説＞ネイピア数＞ネイピア数の定義

ネイピア数の定義

ネイピア数の定義の由来

ネイピア数の定義として次の式が示される場合が多い。
しかし、なぜこの式が定義になっているのかを説明している参考書は少ない。
\[ \displaystyle \lim_{ n \to \infty }(1+\frac{ 1 }{ n })^n=e \]

前ページで、対数の微分の過程で、上記のネイピア数の定義が登場することを解説した。
ここでは、接線の傾きを使ったネイピア数の定義を説明する。

接線の傾きとネイピア数の定義

\(y = a^x\)のグラフで\(x=0\)での接線の傾きが1となるような底aの値をネイピア数\(e\)として定義した。



\(x=0\)のとき、\(y = e^x\)のグラフは\((0,1)\)を通るのだから接線のy切片は1である。
したがって接線の式は次式となる。
\[ y=x+1 \]

上記の接線は点\((0,1)\)と、この点から微少量\(Δt\)だけ離れた点\((Δt,1+Δt)\)を通る。
点\((0,1)\)は\(y = e^x\)と接線の接点でもある。

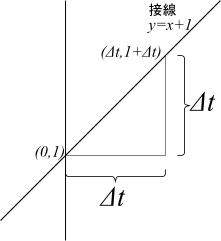
接点\((0,1)\)に無限に近い領域では、\(y = e^x\)と\(y=x+1\)は等しいと見なしてよい。
\(Δt\)が限りなく小さければ、\(y = e^x\)も点\((Δt,1+Δt)\)を含むはずだからである。

そこで、\(Δt\)が無限に小さいことを前提に、\(y = e^x\)と\(y=x+1\)を結びつけ次式を得る。
(代入によりyを消去する)
\[ e^{x}=1+x \]

\(x=Δt\)として代入する。 \[ e^{Δt}=1+Δt \]

この両辺を\( \frac{ 1 }{ Δt }\)乗すると次式となる。
\[ e=(1+Δt)^{\frac{ 1 }{ Δt }} \]

ここで\( \frac{ 1 }{ Δt }=n\)と置く。Δtは無限小なので、\(n\)は無限大になるので次式となる。
\[ e=\displaystyle \lim_{ n \to \infty }(1+\frac{ 1 }{ n })^n \]

上式は冒頭で出てきたネイピア数の定義式である。
このようにネイピア数は接線の式からも導くことができるのだ。

■最初のページ：ピンポイント解説：目次

このページのTOPへ