周期運動
周期運動
同じ動作を繰り返す運動を周期運動という。
周期運動には、円運動、単振動、単振り子がある。
| 円運動 | 天体の公転などが、円運動である。常に中心に向けて力が作用する。これを中心力という。 |
| 単振動 | 円運動を真横から見た状態が単振動である。 |
| 単振り子 | 振れ角が小さい振り子は、単振動となる。 |
繰返し1回分に要する時間を周期、1秒間に繰返される回数を振動数という。
周期と振動数は逆数の関係だ。
円運動
ひもの一方の端にボールを結びつけ、このひもの他端をもってこのボールを振り回したとしよう。
このとき、ボールが描く軌道は円形である。

このように円形の軌道を描く運動を円運動という。
惑星が太陽の周囲を公転する運動も円運動とみなしてよい。(実際は楕円軌道を描いているが)
[..円運動について、さらに詳しく見る]
単振動
バネに取り付いた錘(おもり)の往復運動が単振動だ。
往復運動の方向は、垂直であっても水平であっても、単振動に変わりはない。
バネを少し縮めるためには、少しの力が必要だ。
さらに、縮めるためには、さらに力が必要になる。
伸ばしても同じだ。伸ばせば伸ばすほど、より大きな力が必要になる。

単振動する錘(おもり)の特徴は3つある。
- 振動している間、錘の速度は刻々と変化する
- 振動の両端で、錘の速度は一度ゼロになり、運動の方向を折り返す
- 錘が振動の中央を通過するときのスピードが一番速い
単振り子
糸を結んだ5円玉がユラユラ揺れている状態を想像してみよう。
このユラユラ揺れている状態が単振り子である。

ひもの長さをl、ひもの下端の小球Aの質量をMとする。
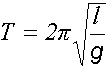
この式の中に登場するg(重力加速度)やπ(円周率)は定数なので人為的に値を変更できない。lのみが実験者の意思で変更可能である。
つまり周期Tは、「糸の長さのみ」で決まってしまうということだ。
小球Aの質量の大小や振幅は、周期には影響しない。
言い換えると、「周期を変えるには、糸の長さを変えるしかない」ということだ。
余談 |
上記は地球上に限定した話だ。 |
■次のページ:円運動
スポンサーリンク
2005/06/03
2016/08/04
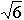 倍になる。(ゆっくり揺れる)
倍になる。(ゆっくり揺れる)