円運動

ひもの一方の端にボールを結びつけ、このひもの他端をもってこのボールを振り回したとしよう。
このとき、ボールが描く軌道は円形である。

このように円形の軌道を描く運動を円運動という。

惑星が太陽の周囲を公転する運動も円運動とみなしてよい。(実際は楕円軌道を描いているが)

円運動には弧度法の理解がかかせない。
ここでは、弧度法について簡単に解説しておこう。

弧度法は角度を測り方の一種だ。
日常的な角度の表記では、一周を360度と決めている。
これに対し、弧度法の一周は2π(=6.2831・・・)となる。

弧度法の威力は孤の長さを測るときに発揮される。
半径r、中心角60度の扇型の弧長を求めてみよう。

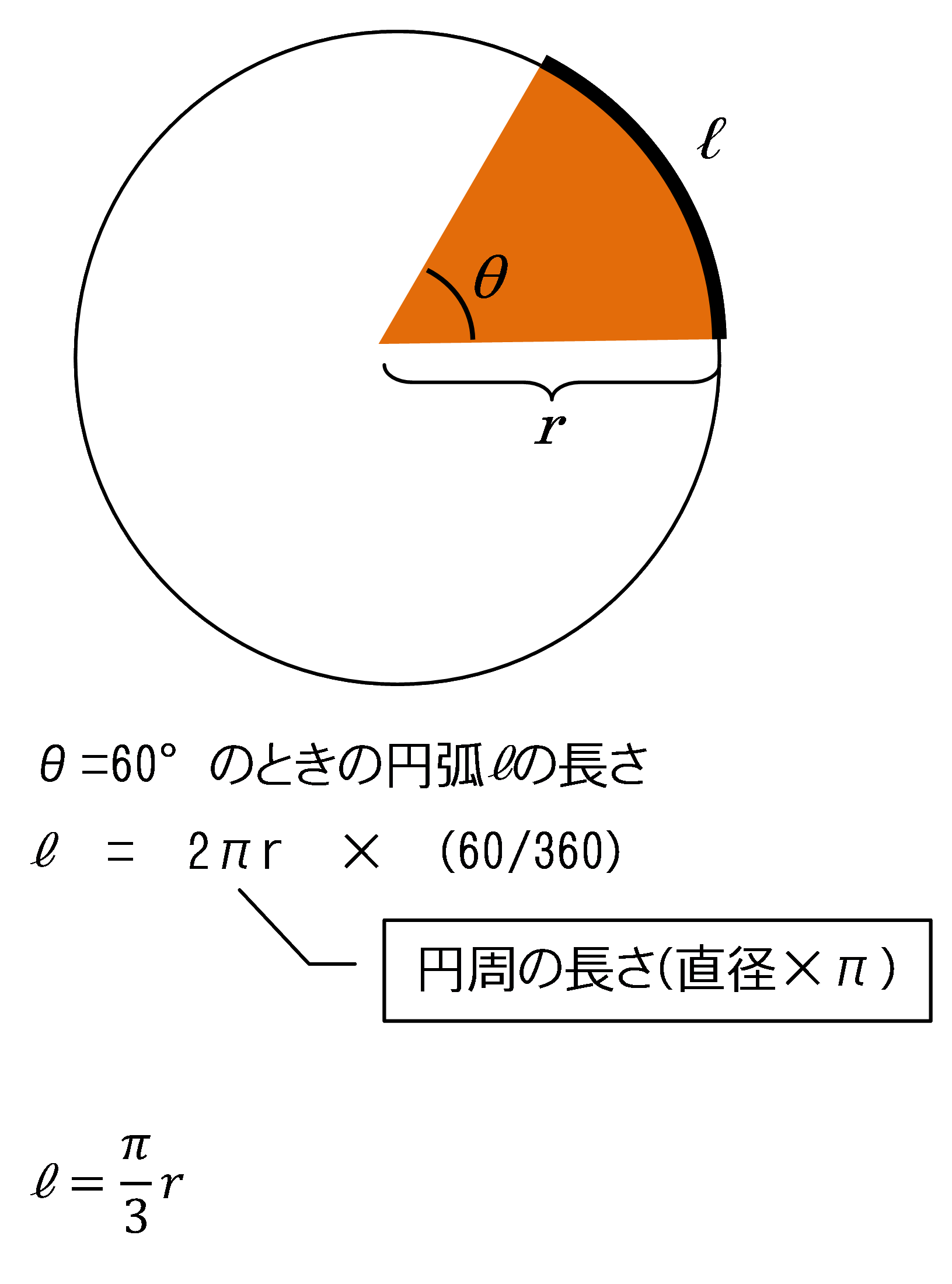
円運動と弧度法

円周の長さ(2πr)と、一周360度に対する中心角の比(60÷360)の積を求めればいい。
つまり、中心角60度の扇型の弧長は(π/3)rということになる。

ところで、60度は弧度法でπ/3だ。弧長は(π/3)にrをかけた形になっているが、これは偶然ではない。

角度と半径の積が、弧長になるように弧度法が定義されているのだ。
繰り返すが、弧長と中心角と半径は次の関係になる。
(弧長) = (弧度法で示した中心角)×(半径)

一周360度を2π(=6.2831・・・)で表現する弧度法の便利さはここにある。

円運動は、直線運動にはなかった角速度と周期が登場する。
角速度は弧度法をベースにすると理解しやすいのだ。

■次のページ：角速度と周期

2005/06/03
2016/09/10