円運動
円運動の加速度
円運動は加速度運動
直線上をぐんぐんスピードアップしながら進む物体があれば、加速しているのは明白だ。
速度の変化が加速度なので、これを加速でないとは言えないだろう。

ところが円運動は、次の図のように円周上を一定の速さで動くので加速しているようには思えない。

しかし円運動は立派な加速度運動なのだ。
円周上を動く質点は円周の接線方向にそのまま直進しようとする速度を持つ。
速度は大きさだけでなく、方向も持ったベクトル量だ。
ベクトルの方向が、直進しようとする方向(接線方向)なのである。
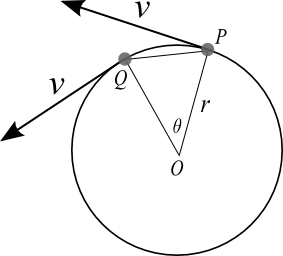
円運動を継続する質点は、実際に直進せず、円周上を周り続ける。
すなわち、直進しようとする方向が刻々と変化するのだ。
これは速度の大きさは変わらないが、速度のベクトルの方向が刻々と変化していることを意味している。
ベクトルが変化しているのは、速度が変化していることにほかならない。つまり加速しているのだ。
この場合の加速は、速度の大きさ(速さ)が変化するのではなく、速度の方向が変化する加速である。
飛び出そうとする速度ベクトルを、飛び出させないように円周にそって向きを変えるのが加速だ。
つまり、円運動の加速の方向は円運動の中心に向かっているのである。
円運動の加速度を求める
ここでは、中心に向かう加速度を導き出してみよう。
円運動をする物体の位置がPからQに変化した。
このとき、速度の大きさvは変わらないが、方向は変化している。

物体を中心として速度の変化を示した図が以下だ。
上の図からP点Q点の速度ベクトルを平行移動して作成している。

△OPQと△O'P'Q'は、頂角をθとする二等辺三角形で合同であるため、直線OP(半径r)は直線O'P'(速度v)と、直線PQは直線P'Q'(速度⊿v)に対応する。
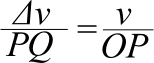
加速度は時間あたりの速度の変化だ。だから速度の変化⊿vを変化した時間⊿tで割れば加速度aとなる。
また極めて短い時間であれば円弧PQと直線PQは同じとみなしてよい。
距離は速さと時間の積だから、直線PQ(円弧PQ)の長さはvに⊿tをかければいい。
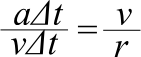
これを整理すると、加速度は速度の二乗を距離で割った値であることが求められた。
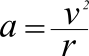
■次のページ:向心力
スポンサーリンク
2016/09/10