力積と運動量
運動量の変化が力積
力とその力が作用した時間との積を力積という。
力が比較的長めに作用した場合の効果を表現した量と考えてもいい。
力の単位は[N]、すなわち[kg・m/s2]である。
これと時間との積が力積なのだから、力積の単位は[kg・m/s]となる。
この単位をご記憶だろうか?
[kg・m/s]は運動量の単位でもある。
運動量と力積とは本質が同等なのである。
力が作用すると運動量が変化すると解説した。詳しく言い換えると
運動量の変化は、与えられた力積に等しい
といえる。
運動量p1の質点に、力Fが時間tの間作用した場合、その後の運動量はp1+F tとなる。
このイメージはこうだ。コロコロとゆっくり転がるゴルフボールを、ごく微量な力で後押しする。
このとき、
ケース1:一瞬だけ後押しする。
ケース2:5秒間継続して後押しする。
の二つを考える。
Aが力を受けるのは一瞬だが、Bは力を受けつつづける。
その結果、Bの方がより大きな速度を得るということだ。
これが力積の作用である。
数式で確認してみよう。
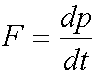
無論、力積が作用し運動量が変化した場合であっても、力積を与えたものと与えられたものとの間で運動量保存の法則は成り立っている。
■最初のページ:質点の力学:目次
スポンサーリンク
2005/06/03
2007/11/19