剛体の力学

外積の大きさ

まず、大きさから解説しよう。
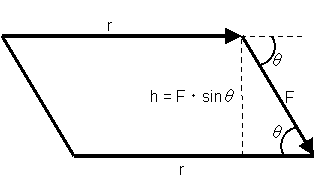
力のモーメントＮを例にすると、大きさは以下の式で表現される。
N=rF・sinθ
これは理解しやすい。
Nの大きさは「Fとrが作る平行四辺形の面積」と同じなのだ。

余談 rF・sinθがなぜ平行四辺形の面積になるのか、念のために確認しておこう。 平行四辺形の面積は「底辺 × 高さ」だ。 下図で底辺をr、高さをhとすると、面積はr hである。 hはF・sinθと等しいので、結局面積はr F・sinθということになる。

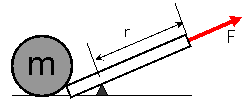
Fとrが同じ方向の場合は、sinθがゼロなので、Nはゼロ、つまり回転させる効果はまったくないということだ。
てこを例にすると、柄の方向に引っ張ることになる。
これでは、てこは用をなさない。

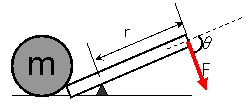
Nが最大になるのは、Fとrが直角の場合である。
てこを例にすると、柄と直角の方向に、力をかければ、てこを回転させる効果(物体を動かそうとする効果)が最も大きくなるのである。

角度θとNの大きさの関係をまとめると、以下の表になる。

θ=0 Fとrが同じ方向	0<θ<90	θ=90 Fとrが直角
面積は0	面積はr F・sinθ	面積はr F
N = 0 θ=0でＮは最小	N = r F・sinθ	N = rF θ=90でＮは最大

2005/06/25

前ページ	このページの先頭	次ページ
物理の基礎基本・試験対策・レポート対策
物理学解体新書・HOME