力のモーメント
力のモーメントとは
物体を回転させようとする作用が力のモーメントだ。
てこの原理、滑車の原理は力のモーメントの典型例である。
ここでは、力のモーメントについて、細かに解説する。
剛体を回転させようとする能力は、力の大きさFだけでなく作用線と回転の中心との距離rにも比例する。
Fが大きいほど、rが長いほど、剛体を回転させようとする能力は高いのだ。
物体を回転させようとする能力を力のモーメントNといい、Fとrの外積で表す。
外積なので、力のモーメントはベクトル量なのだ。
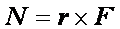
力のモーメントは別名トルクともいう。
力のモーメントはてこの原理と重ね合わせると理解しやすい。
てこでは、柄が長いほど、また力をかけるほど、物体を動かす効果が大きくなる。
柄の長さがr、かける力がFに該当する。
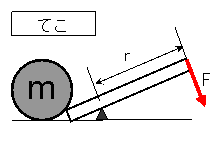
つまり、より柄の長いてこを使い、より大きな力をかけると、よりおおきな力のモーメントが得られるので、重い物体でも動かしやすくなる(てこが回転しやすくなる)ということだ。
力のモーメントはまさに「物体を回転させようとする能力」なのだ。
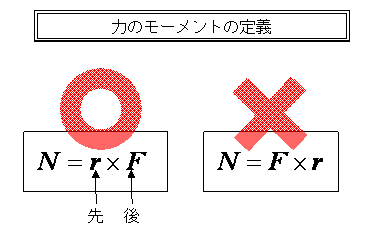
後述するが、かける順序を誤らないで欲しい。rが先、Fが後とするのが定義だ。
かける順番が変わると、符号も変わるのが外積の特徴である。
符号が変わると、方向が逆になるし、答えも違ってくるということだ。
力のモーメントが打ち消しあうと、物体は停止したまま回転することはできない。
これは、「ついあいの条件」で解説する。
力のモーメントがベクトルであることに、違和感を覚えることもあると思う。
力のモーメントをなぜ、ベクトルで扱うのかについては「力のモーメントの違和感」で解説する。
■次のページ:力のモーメントの違和感
スポンサーリンク
2005/06/25