デュロン=プティの法則
デュロン=プティの法則
デュロン=プティの法則とは
世の中には、温まりやすい物体と温まりにくい物体がある。
物体の温まりやすさの指標を比熱容量といい、物体1kgの温度を1℃上昇させるために必要な熱量で示す。単位は[ J/kg・K]だ。
慣用として、比熱という語が使用される場合があるが、比熱容量が正しい。
比熱容量の値は、物質により当然異なる。
熱し難く冷めにくい物質の代表は水である。
その比熱容量の値は、4.184×103[ J/kg・K]と大きい。
比熱容量に対してモル熱容量という物理量もある。
モル熱容量は、物体1モルの温度を1℃上昇させるために必要な熱量を意味し、単位は[J/(mol・K)]である。
また、体積を一定に保ったまま測定したものを「定積モル熱容量Cv」、圧力を一定に保ったまま測定したものを「定圧モル熱容量Cp」という。
比熱容量は物体によって異なるが、固体の定積モル熱容量は物質の種類とは無関係に「だいたい同じ」になる。
その値は約25.5[J/mol・K]だ。
これを、デュロン=プティの法則という。
この法則はデュロン(P.L.Dulong)とプティ(A.T.Petit)が独立に発見し、1819年に発表したものだ。
どの固体でも定積モル熱容量は、みな同じなのである。
だから、「未知の固体の定積モル熱容量を測定したら約25.5[J/mol・K]でした。この物体は何でしょうか?」と質問されても答えようがないのだ。
デュロン=プティの法則と気体定数
気体の状態方程式に登場するRを気体定数という。
その値は8.31[J/ mol・K]だ。
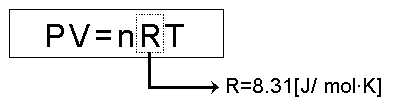
気体定数を見ると、単位[J/ mol・K]が、定積モル熱容量と同じであることに気が付く。
固体の定積モル熱容量:約25.5[J/mol・K]は、ちょうど3R(気体定数Rの3倍)に相当する。
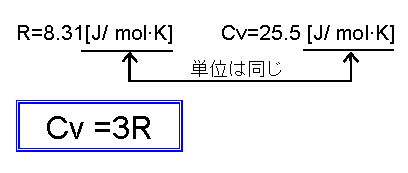
この一致は単なる偶然ではなく、キチンとした理論的根拠があるのだ。
固体内の原子は、規則正しく整然と並んでいる。
しかし、完全に静止しているのではなく平衡の位置を中心として小さく振動しているのだ。
原子は周囲の原子と隣接しているので、相互に力を及ぼしあい、常に平衡位置に戻ろうとする。
つまり、個々の原子の振動は直線上の運動ではなく、3次元の広がりを持ったものだ。
各原子は皆、バネで連結されているとイメージすると理解しやすい。
1つの原子の振動は、3つの調和振動子(単振動をする質点)が集まったものとみなすことができる。
3次元の広がりを各次元に分解するからだ。
固体全体がN個の原子で構成されている場合、この固体は3N個の調和振動子を含んでいることになる。
ここで、いよいよ登場するのが「温度Tの熱平衡状態にある系では、各自由度の運動エネルギーの平均はkT/2である」というエネルギー等分配の法則だ。
なお、kをボルツマン定数と呼ぶ。
ボルツマン定数とは、気体定数Rをアボガドロ数Naで除したものを指す。
1つの調和振動子が1つの自由度に相当するので、1つの原子は3kT/2の運動エネルギーを持つことになる。
1つの原子の自由度は3だからだ。
調和振動子は、運動エネルギーだけではなく位置エネルギーも持つ。
調和振動子の場合、位置エネルギーの平均値は運動エネルギーの平均値と等しい。
つまり、1つの原子のエネルギーは、運動エネルギー3kT/2と位置エネルギー3kT/2を合計した値3kTになる。
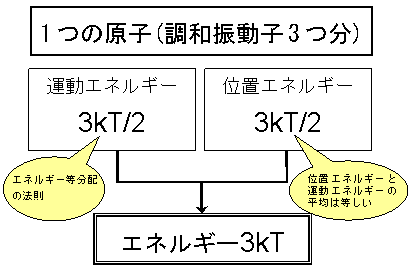
固体中の原子数はN個なので、この固体が持つエネルギーUは、3NkTになる。
ここでは、原子の数をNa個と考えよう。Naはアボガドロ数だ。
つまり、固体1モルあたりが持つエネルギーUは、U=3NakTになるのだ。
1モルあたりのエネルギーUを温度で割れば、モル熱容量Cvとなる。
さらに、NakはRなので、Cv=3Rとなる。
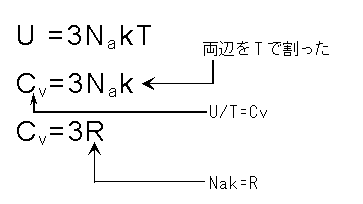
この式から、定積モル熱容量は固体の種類や質量、温度に無関係であることが読み取れる。
ここで、デュロン=プティの法則を再度表現しなおこう。
すべての固体は3Rに等しい定積モル熱容量を持つ。
デュロン=プティの法則は極低温で通用しなくなる。
次ページで極低温でのデュロン=プティの法則を解説する。
■次のページ:デュロン=プティの法則と極低温
スポンサーリンク
2006/09/13