データ処理の知識
| 項目名 | 内容 |
| 誤差 | 測定値のばらつき具合を示す |
| 有効数字 | 信用していい計測値の範囲を示す |
| 最小二乗法 | プロットに対して、妥当な直線を引く |
| グラフ |
誤差
どんなに高精度の計測器を使用しても、真の値をズバリ読み取ることはできない。
計測するときは、「真の値」を読んでいるのではなく、真の値の近くを読んでいるのだ。
だから、ある量を何回か測定すると、毎回違った値になる。
真の値と、測定値との差を誤差という。
誤差は様々な要因で生じる。
要因によって誤差を分類すると以下のようになる。
| 誤差の種類 | 略説 | |
| 過失誤差 | うっかりしたミス、単純ミスによる誤差 | |
| 系統誤差 | 器械的誤差 | 計測器に起因する誤差 |
| 理論的誤差 | 理論と現実とのギャップに起因する誤差 | |
| 個人的誤差 | 実験者の個人差に起因する誤差 | |
| 偶然誤差 | 周囲の環境による偶発的な誤差。 偶然誤差には誤差の3公理が存在する。 |
|
有効数字
有効数字の最小桁は、目分量で読み取られた数値である。
従って、有効数字は「常に最小桁に不確かさが付きまとう数値」と認識しておく必要がある。
「有効」という言葉から、「有効数字は全桁が正確」といった印象を持つ人がいるが、それは誤りである。
有効数字は、最小目盛りの1/10の範囲で不確かさが含まれた数字なのだ。
繰り返すが、測定で真の値を知ることはできない。
しかし、目分量での読み取りが適切に行われていれば、真の値は最小目盛りの1/10の幅に入っていることになる。
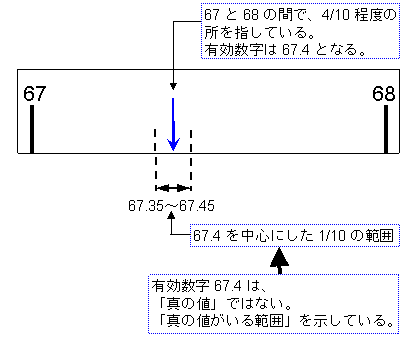
例えば、有効数字が「67.4」であったとする。最小桁の「4」は目分量で得た値だ。
目分量の幅は1/10なので、真の値は67.35〜67.45の範囲に入っているはずだ。
最小自乗法
実験で得た測定値をグラフ上にプロットしても、それらがキレイに一直線に並ぶことはまずない。
個々の測定値には誤差が含まれるからだ。
そこで、「たぶん、この辺がバラツキの中央だろう」と見込みをつけて、感覚で直線を引くことになる。
直線を引いてみると、たまたま直線に重なったプロットもあれば、極端に離れたプロットもいることだろう。
サンプル数(測定の回数)が多ければ、プロットの多くは直線の周囲に密集することになる。
しかし、直線を引く感覚は人によって、異なるはずだ。
同じ測定結果であっても、「この辺が中央だ」という見込みが人の感覚によって変わってくるのである。
同一のプロットなのに、人によってy切片や傾きが異なる直線が導かれるのだ。
ただでさえ、測定結果には誤差が付きものなのに、さらに直線の引き方が人によってバラつくのでは、実験の精度は下がるばかりだ。
そこで、「人による直線の引き方の違いをゼロにする方法」が考案された。
これが最小自乗法である。
スポンサーリンク
2005/09/04
2009/12/18
物理の基礎基本・試験対策・レポート対策 |
||
物理学解体新書・HOME |
||
|
|
||
