最小二乗法
実験で得た測定値をグラフ上にプロットしても、それらがキレイに一直線に並ぶことはまずない。
個々の測定値には誤差が含まれるからだ。
そこで、「たぶん、この辺がバラツキの中央だろう」と見込みをつけて、感覚で直線を引くことになる。
直線を引いてみると、たまたま直線に重なったプロットもあれば、極端に離れたプロットもいることだろう。
サンプル数(測定の回数)が多ければ、プロットの多くは直線の周囲に密集することになる。
しかし、直線を引く感覚は人によって、異なるはずだ。
同じ測定結果であっても、「この辺が中央だ」という見込みが人の感覚によって変わってくるのである。
同一のプロットなのに、人によってy切片や傾きが異なる直線が導かれるのだ。
ただでさえ、測定結果には誤差が付きものなのに、さらに直線の引き方が人によってバラつくのでは、実験の精度は下がるばかりだ。
そこで、「人による直線の引き方の違いをゼロにする方法」が考案された。
これが最小自乗法である。
最小自乗法は、実験で得た測定値から計算によって直線の式(y=ax+b)を導き出す。
この直線の式に従ってグラフ上に直線を引けば、「バラツキの中央」にズバリ一致した直線を引くことができるのである。
最小自乗法は、計算だけで直線を決めるので人の「慣れ」や「癖」には無関係に「バラツキの中央」を通る直線が引けるのだ。
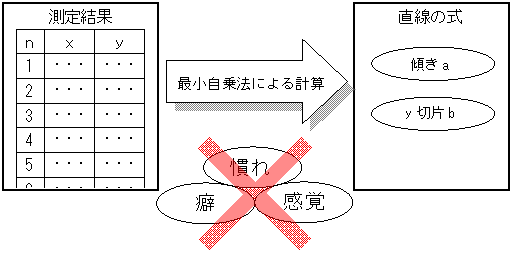
人の感覚による直線は、プロットのバラツキの様子を見て直線を引く。
つまり、直線よりも先にプロットがなければ引くことができない。
ところが最小自乗法ではプロットを見る必要はない。
測定値をプロットするよりも先に、グラフ上にまず直線を引き、その後から測定値をプロットすることも(メリットがあるかどうかは別として)可能なのだ。
つまり、最小自乗法では、グラフ上に直線を引く人の「慣れ」や「癖」には無関係に直線が引けるのである。
最小自乗法で得られた直線の式を実験式という。
実験式は背景となる物理法則とは無関係だ。
測定値のみから自動的に算出されるからだ。
これに対し、物理法則から、導出された式を理論式という。
では、最小自乗法により実験式の「傾きa」と「y切片b」を算出する計算方法を見てみよう。
シグマが登場するので腰が引けるが、よく見ると、この式で使用する変数は次のものしかない。
- ・サンプル数
- ・xの合計値
- ・yの合計値
- ・xyの合計値
- ・x2の合計値
上記でリストアップした言葉を使って式を書き直すと
このように書くと、最小自乗法の計算も意外と簡単なことが分かる。しかも、aとbで分母は同じなのだ。
測定結果を表にまとめるときに、x、yの値だけでなく、xy・x2の欄も設け、それぞれ合計値も記入すれば分かりやすい。
下表の例では、色を付けた部分が、最小自乗法の式に登場する変数である。
理論式の直線と実験式の直線を比較すると、考察のヒントになる。
理論式の直線に対し、実験式の直線が並行にシフトしていれば、計測器のゼロ点補正が怪しかったと考察できる。
例えば、
「理論式の直線と実験式の直線の傾きを比較すると、両者は0.2%しか違わない。一方でy切片は○○％も異なる。
このことから、実験に使用した○○計のゼロ点が正しく補正されていなかった可能性が考えられる。
"実験の手順"に記した通り、実験開始時にゼロ点は補正したが、実験中、および実験終了時にゼロ点は確認しなかった。
このような実験誤差を排除する対策として、実験開始時だけでなく、実験中・実験終了時にもゼロ点を確認し必要に応じて補正することが考えられる」
などと書く。
スポンサーリンク
2005/09/04
物理の基礎基本・試験対策・レポート対策 |
||
物理学解体新書・HOME |
||
|
|
||