有効数字

HOME＞ 実験レポートの書き方＞データ処理の知識＞有効数字

有効数字とは

「2.50」と「2.5」はまったく違う値

有効数字とは、計測器で測った値をどの桁まで信じるかを表す数字である。
測定値を読み取るときに「最小目盛りの1/10の値を目分量で読む」というルールがある。
このルールに従って読み取った値が有効数字だ。

有効数字は、最小桁に1/10の不確かさが付きまとう数値なのである。
ここでは、なぜ有効数字が使われるのか、有効数字の考えたかについて根本から解説する。

小学校の算数では、「2.50」は末尾の「0」を取り去って「2.5」と書くように教えている。
「2.50」も「2.5」も同じだから末尾の「0」はいらないのだ。

しかし、有効数字では「2.50」と「2.5」は違うものと考える。
有効数字を理解するためには、まず小学校の算数を忘れる必要がある。

有効数字を理解するために、測定値を読み取るルールから確認しよう。

有効数字：測定値を読み取るルール

実験には測定が伴う。例えば以下のケースがある。
・テスターで電圧を測定する。
・メスシリンダーで溶液の体積を測定する。
・温度計で温度を測定する。

このような測定では、必ず目盛りを読んで測定値を知る。
ここで、問題が生じる。
テスターの針や、メスシリンダー内の水面等は、目盛りと目盛りの間になる場合が多いということだ。(下図)

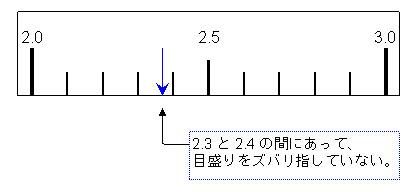
そこで測定値を読み取るときに「最小目盛りの1/10の値を目分量で読む」というルールを設ける。
例えば次の図のようになる。

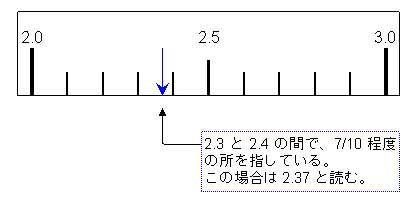
もし最小目盛りが0.1Vであれば0.01Vまで、0. 01Vであれば0. 001Vまで読み取ることになる。
つまり、計測器の最小目盛りの精度が上がるほど、より精密な測定が可能になるということだ。

このルールを適用すると、目盛りをズバリ指している場合も、1/10の値まで読み取る必要がある。

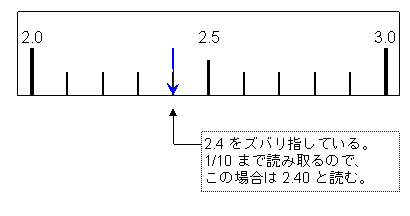
この例では、2.4をズバリ指しているからと言って、「2.4」と読んではいけない。
1/10の値まで読むので「2.40」と読み取る。

このようにして読んだ「最小目盛りの1/10までの値」を有効数字という。

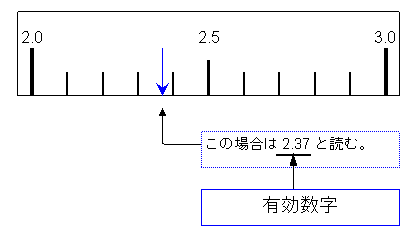
ここで注意を要する。
どんなに高精度の計測器を使用しても、真の値をズバリ読み取ることはできない。
無限に細かい目盛りは存在しないからだ。
だから「真の値は、最小目盛りの1/10の値の付近にいるはずだ」としか言えないのだ。
計測は真の値を読んでいるのではないのだ。

有効数字：測定値をどの桁まで信用するか

有効数字の最小桁は、目分量で読み取られた数値である。
従って、有効数字は「常に最小桁に不確かさが付きまとう数値」と認識しておく必要がある。
「有効」という言葉から、「有効数字は全桁が正確」といった印象を持つ人がいるが、それは誤りである。
有効数字は、最小目盛りの1/10の範囲で不確かさが含まれた数字なのだ。

繰り返すが、測定で真の値を知ることはできない。
しかし、目分量での読み取りが適切に行われていれば、真の値は最小目盛りの1/10の幅に入っていることになる。
例えば、有効数字が「67.4」であったとする。最小桁の「4」は目分量で得た値だ。
目分量の幅は1/10なので、真の値は67.35〜67.45の範囲に入っているはずだ。

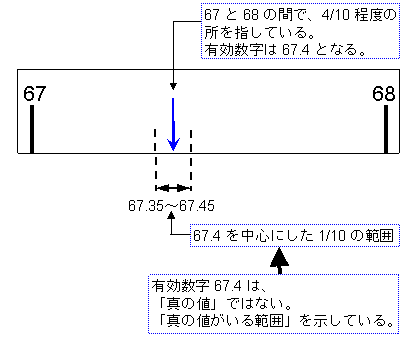
有効数字が「67.4」であるということは、「67.35〜67.45の範囲」を代表して「67.4」と表現しているに過ぎない。

有効数字が決まれば、自然と「真の値はこの中に入っていますよ」という範囲が決まるのだ。
有効数字を見ることによって、値だけでなく、その値をどこまで信じていいのかが歴然とする。真の値の範囲が分かるからだ。

計測するときは、「真の値」を読んでいるのではなく、「真の値がいるはずの範囲」を読んでいるという事実を意識しなくてはならない。

有効数字は単なる測定値ではなく、「どこまで信じていいのか」という範囲も含まれた表現なのだ。
測定中や、レポート制作中は、特に有効数字の意味を忘れてはならない。

■次のページ：有効数字の読み取り時の注意

このページのTOPへ