有効数字
HOME> 実験レポートの書き方>データ処理の知識>有効数字
有効数字の計算処理
計算の基本は加減乗除である。
加減乗除によって、和差積商が得られる。
加減乗除を経ることによって、有効数字の桁数が変化する。
つまり「真の値が含まれる範囲」が広がるのだ。これは数値の精度が低下することを意味する。
ここを意識して適切な処置をしないと、計算値はあっていても、「真の値が含まれる範囲」が違ってきてしまう。
これでは正しいデータ解析とは言えない。
ここでは和差積商を求める場合の有効数字の扱いについて解説する。
和の場合
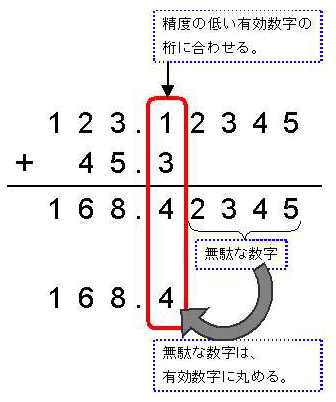
123.12345gの溶液に、45.3gの同種の液体を加えるとする。
この場合は精度の悪い方の有効数字に合わせて計算する。
精度の良い値と、精度の低い値を合計したら、答えは精度が低い方に埋もれてしまうからだ。
| 正誤 | 計算式 | 解説 |
| ×:誤 | 123.12345+45.3=168.42345 | 計算後に精度が高くなることはあり得ない。 |
| ○:正 | 123.12345+45.3=168.4 | 精度が低い数値が全体の精度を決める。 |
有効数字よりも細かな数字は、無駄なので、有効数字の桁数に丸めなくてはならない。
差の場合
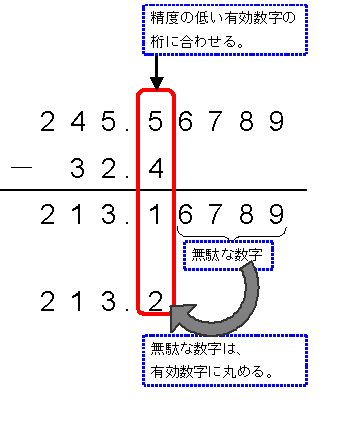
245.56789gの溶液から、32.4gを取り去るとする。
この場合は精度の悪い方の有効数字に合わせて計算する。
精度の良い値と、精度の低い値を合計したら、答えは精度が低い方に埋もれてしまうからだ。
| 正誤 | 計算式 | 解説 |
| ×:誤 | 245.56789-32.4=213.16789 | 計算後に精度が高くなることはあり得ない。 |
| ○:正 | 245.56789-32.4=213.2 | 精度が低い数値が全体の精度を決める。 |
有効数字よりも細かな数字は、無駄なので、有効数字の桁数に丸めなくてはならない。
■次のページ:有効数字:数値の丸め方
スポンサーリンク
2005/09/26
2009/12/16