力のつり合い

HOME＞ 質点の力学＞力のつい合い

力のつり合いとは

一つの質点mに複数の力が加わっているとする。
これら力のベクトルの和がF(F≠0)のとき、この質点はF/mの加速度を得て移動する。(運動の第二法則)
つまり、複数の力が加わっていても合成された力のみが質点に作用していると考えていいのだ。

さて、力のベクトルの和Fが0の場合はどうなるのか？
加速度が加わらないため、質点は静止したまま(または等速直線運動のまま)を維持することになる。

複数の力が同時に加わっても、その合力が0の場合は、その質点は何らの力の作用を受けていないのと同じことになる。
このとき、力はつりあっているという。

ここでは、力のつりあいについて、細かく説明しよう。

力のつり合いはベクトルで表現

物体に二つの力F1とF2が作用している。

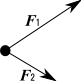
このような場合は、二つの力は合成されて、まるで一つの力のように見える。

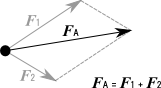
ここでは、F1とF2を合成してFAとしよう。
力の合成は足し算として表現することができる。
力はベクトル量だからである。

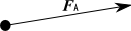
ここで、FAと等大逆向きの力F3を物体に与える。
この結果、物体にかかる合力はゼロになる。

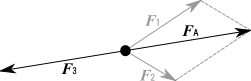
このとき、二つの力の関係は
FA ＝−F3
となる。


F3にマイナスが付くのは、FAの逆向きだからだ。
もし、マイナスがなければ同じ向きになってしまう。

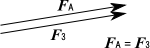
もともと、FAはF1とF2の合成であった。
従って、次のような関係になる。

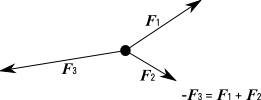
F1、F2、F3は、向きも、大きさも異なった力である。
しかし、この三つの力が同時に作用した結果、合力はゼロになる。

このように、複数の力が同時に作用して、合力がゼロになった状態を力がつりあっていると表現する。
力がつりあっている状態では、力が作用していないのと同じだ。

加速度が加わらないため、質点は静止したまま(または等速直線運動のまま)を維持することになる。

作用・反作用の法則は、力のつり合いと間違いやすい。次のページでは、力のつり合いと作用・反作用の違いを解説する。

■次のページ：力のつり合いと作用・反作用

このページのTOPへ