単振動

単振動の式

錘の位置を時間tで2回微分すると錘の加速度が得られる。
この加速度と質量の積が力であり、バネ弾性力に相当する。
これを運動方程式で表すと次のようになる。

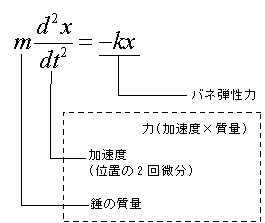
これが単振動の式を得るための微分方程式だ。
この式を見ると、「xを2回微分したらマイナスxになる」ということに気が付く。

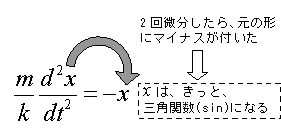
2回微分すると元の形にマイナスが付く関数は、sinだ。
このことから「単振動の式は三角関数になるに違いない」と見通すことができる。

質量m、バネ定数kを使用して、ω(オメガ)を以下のように定義しよう。

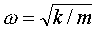
これを代入すると、次の式になる。

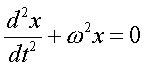
この式のパターンは微分方程式の基本形(線形2階微分方程式)だ。
A、αを定数とすると、この微分方程式の一般解は次の式になる。
つまり、これが単振動を表現する式なのだ。

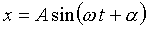
この式は、単純な三角関数である。
三角関数は繰り返しの関数なので、この式は「単振動は繰り返す運動」であることを示唆している。

さて、単振動を決める各変数について解説しよう。
変数は、振幅、角振動数(角周波数)、位相、初期位相、振動数、周期だ。

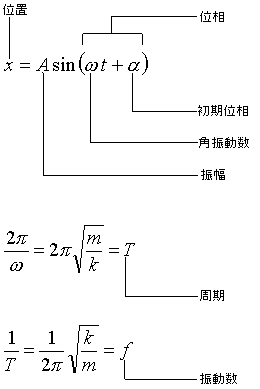
振幅	振幅は、振動の中央から振動の限界までの距離を示す。限界から限界までの全幅ではない。
位相	位相は、質点(上記の例では錘)の位置を角度で示したものである。 sinの中にいるので、位相は角度で表される。
初期位相	単振動をスタートするとき、錘を中心からちょっとズラして、後はバネ弾性力にまかせて運動させる。この「スタート時(初期)に、ちょっとズラした程度」を初期位相という。初期位相は角度で表される。
角振動数	位置の変化を、角度の変化で表現したものを角振動数という。角度の変化は時間あたりの変化で示す。
周期	周期は一往復にかかる時間を示す。周期2[s]であったら、その運動は2秒で1往復する。周期は振動数の逆数である。
振動数	振動数は、1秒間あたりの往復回数である。単位はHz(ヘルツ)である。振動数2[Hz]であったら、その運動は1秒で2往復する。振動数は周期の逆数である。

垂直に単振動するのであれば、重力mgも運動方程式に入るのではないかとう疑問もある。
その通り、重力mgも運動方程式に入れるべきなのだ。
ただし、重力とバネ弾性力がつりあった場所を原点(x=0)として単振動するので、結局、単振動の式は同じになるのである。

2005/06/03
2006/09/20
2016/09/12