単振り子

HOME＞ 質点の力学＞単振り子＞単振り子の向心力

単振り子の向心力

単振り子の向心力を導出する

単振り子は両端で速度ゼロとなり、原点を通過するときの速さが最大となる。
これは、原点から離れる(両端に近づく)ほど、原点に引き戻そうとする力(向心力)が強まることを意味している。
反対に、原点を通過する瞬間は最大の速さだが、向心力は作用していない。

質量\(m\) の球体が、長さ\(l\) の糸につるされた単振り子がある。
この球体には重力\(mg\) が作用しているが、そのまま落下しないのは、糸が張力\(S\) で球体を引いているからだ。
球体は揺れているため、\(mg\) と\(S\) は直線上にならず、糸の角度\(θ\) だけずれてしまう。
\(mg\) と\(S\) の合力が球体に作用する力\(F\) となる。

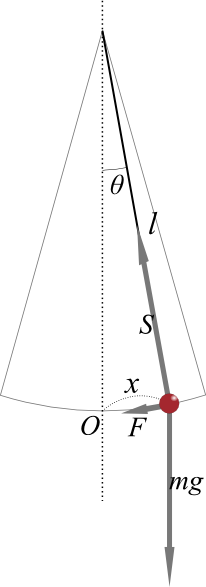
合力\(F\) は\(mg\) と\(S\) が作る平行四辺形の対角線になることから、次式となることが分かる。
\[ F=-mg\sin \theta・・・・・・・・・(1) \] この式を見ると、合力\(F\)は一定ではなく球体の位置で決まることが読み取れる。
球体が動けば、\(θ\) が変化するからだ。

球体が原点を通過するとき(\(θ=0\))のとき、合力\(F\)はゼロとなる。
反対に、球体が最大に振れたとき(原点から最も離れたとき)に、合力\(F\)の大きさが最大になる。

さらに、マイナスが付いているのは\(F\)が常に原点を向いていることを示している。
例えば、球体に右に振れれば角度\(θ\)はプラスだが、力はプラスの方向ではなく原点を向いている。
だからマイナスなのだ。

つまり、合力\(F\)は常に球体を原点に引き戻す方向に作用するのである。
この力を向心力という。 単振り子を揺らす力が向心力なのだ。

角度\(θ\) が小さいとき、\(\sin \theta\) は次式のように、ほぼ \(θ\)とみなしてよい。
\[ \sin \theta\fallingdotseq\theta \]

上記の関係から合力の式(1)は、\(\sin \theta\) を、\(\theta\)に置き換えて、
\[ F=-mg \theta・・・・・・・・・(2) \] となる。

弧度法で角度を示すと、(角度)×(半径)＝(弧長)の関係が得られることから、球体の位置xは、次式で表すことができる。
\[ x=l \theta \]

これを合力の式(2)に代入すると、次式となる。
\[ F=-m \frac{ g }{ l }x \] これが単振り子の向心力Fの式である。

単振り子は揺れている。だから位置xは刻々と変化する。
向心力Fは、揺れている最中、常に変化しているのだ。

■次のページ：単振り子の周期

このページのTOPへ