角運動量

HOME＞ 剛体の力学＞角運動量＞角運動量と力のモーメント

角運動量と力のモーメント

角運動量の式の両辺を時間tで微分してみよう。

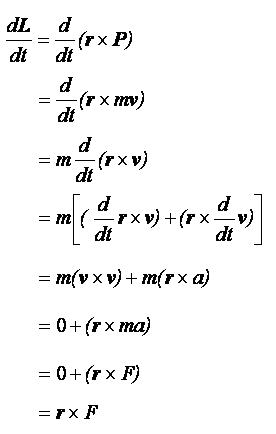
角運動量を時間で微分すると、力のモーメントになった。
つまり、角運動量の時間変化が力のモーメントに相当するということだ。

このことを、並進運動と対比してみよう。

運動	並進運動	回転運動
式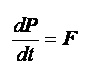
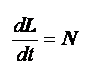式の意味	運動量の時間変化が力に相当する。	角運動量の時間変化が力のモーメントに相当する。
式の解釈	加える力が大きいほど、運動量の変化は大きい。 運動量の大きな物体を急停止するには、大きな力が必要である。 小さな力であっても、時間をかければ、運動量の大きな物体を減速させることができる。	加える力のモーメントが大きいほど、角運動量の変化は大きい。 角運動量の大きな物体の回転を急停止するには、大きな力のモーメントが必要である。 小さな力のモーメントであっても、時間をかければ、角運動量の大きな物体の回転を減速させることができる。

■次のページ：並進運動と回転運動の比較

このページのTOPへ