角運動量
角運動量
角運動量とは
並進運動での運動量に対応するのが、角運動量だ。
運動の勢いの程度が運動量であるように、角運動量は回転運動の勢いとみなしていいだろう。
物体が運動量Pで回転運動しているとき、回転の中心からの距離rとPとの外積を角運動量という。
外積ということは、角運動量はベクトル量なのだ。
角運動量は一般にLで表現する。
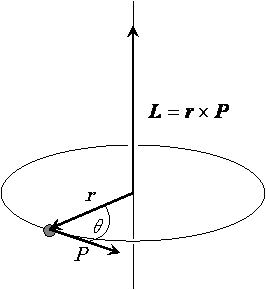
上図から分かるように力のモーメント(トルク)と角運動量は定義が似ている。
混同することのないようにお願いしたい。
力のモーメントに対して、角運動量を「運動量のモーメント」と呼べば、誤解や混乱は少ないと思う。
「イメージは「運動量のモーメント」であるが、正式には「角運動量」と呼ぶ」と認識しておけば、間違いにくい。

角運動量の定義は分かったが、これが何の役にたつのか、といった疑問もあると思う。
次ページ以降で、角運動量の意味を順次しよう。
角運動量と力のモーメント
角運動量の式の両辺を時間tで微分してみよう。
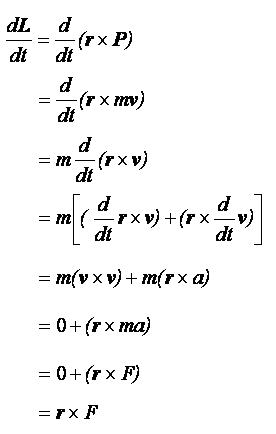
角運動量を時間で微分すると、力のモーメントになった。
つまり、角運動量の時間変化が力のモーメントに相当するということだ。
このことを、並進運動と対比してみよう。
| 運動 | 並進運動 | 回転運動 |
| 式 | 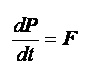 |
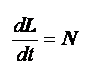 |
| 式の意味 | 運動量の時間変化が力に相当する。 | 角運動量の時間変化が力のモーメントに相当する。 |
| 式の解釈 | 加える力が大きいほど、運動量の変化は大きい。 運動量の大きな物体を急停止するには、大きな力が必要である。 小さな力であっても、時間をかければ、運動量の大きな物体を減速させることができる。 |
加える力のモーメントが大きいほど、角運動量の変化は大きい。 角運動量の大きな物体の回転を急停止するには、大きな力のモーメントが必要である。 小さな力のモーメントであっても、時間をかければ、角運動量の大きな物体の回転を減速させることができる。 |
角運動量と慣性モーメント
角運動量を、回転半径と運動量の外積で表現した。
その他に、慣性モーメントと角速度の積で表現する方法もある。
| 回転半径と運動量の外積で表現 | L=r×P |
| 慣性モーメントと角速度の積で表現 | L=Iω |
繰り返すが、並進運動と回転運動は対応して考えると理解しやすい。
角運動量に関する物理特性を、並進運動と回転運動で比較しておこう。
| 運動 | 並進運動 | 回転運動 |
| 式 | P=mv | L=Iω |
| 式の意味 | 質量(慣性質量)と速度の積が運動量である。 | 慣性モーメントと角速度の積が角運動量である。 |
| 式の解釈 | 質量が小さくても、速度が速ければ運動量が大きい。(例:銃弾) 速度が遅くても、質量が大きければ、運動量は大きい。 |
慣性モーメントが小さくても、角速度が速ければ角運動量が大きい。 角速度が遅くても、慣性モーメントが大きければ、角運動量は大きい。 |
角運動量保存の法則
角運動量が保存されているということは、ベクトルの方向(軸の方向)も一定ということだ。
軸は回転面に常に垂直なので、軸の方向が一定であれば回転面も一定である。
惑星の軌道が平面内に収まっているのは、公転時に角運動量が保存され、公転軸が一定だからである。
■次のページ:角運動量と力のモーメント
スポンサーリンク
2005/07/03