角度に関する量:角度

角度に関する量

並進運動では、移動の程度を位置で表現した。
回転運動では、回転の程度を角度で示す。

角度は、並進運動での位置に相当する。
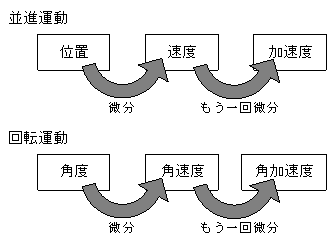
位置を時間で微分して速度が、さらに微分して加速度が求められた。
同様に、角度を時間で微分すると角速度が、もう一度微分すると角加速度が得られる。

角速度

回転する円盤を考えてみよう。
回転する速度は中心からの距離によって異なる。
外側に行くほど速度は速い。

円盤上の場所によって速度が異なるのであれば、速度を使って回転スピードを示すと具合が悪い。

回転スピードには、円盤が回転しても場所によって同一な物理量を使用したい。
それには角度を利用した物理量が適切だろう。
単位時間あたりに、どの程度回転したかを角度で示せばよい。
これが角速度だ。

刻々と変化する角度を時間で微分すると角速度になる。
角速度は一般にω(オメガ)で示す。
[..角速度についての詳しい説明..]

直線運動する物体のスピードがだんだんと速くなっていく場合、加速度を持つという。
同様に、回転する物体の角速度がだんだんと速くなっていく場合、角加速度を持つという。

角加速度は、単位時間あたりの角速度の変化である。
だんだん回転が遅くなっていけば、それはマイナスの角加速度である。
角加速度は一般にα(アルファ)で示す。

■次のページ：角速度

2005/07/03