仕事と仕事率

HOME＞ ピンポイント解説＞仕事と仕事率＞仕事の定義＞力と移動方向が異なる場

力と移動方向が異なる場

今度は斜めに力を加えた場合を考えよう。
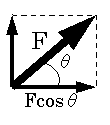
移動方向に対して角度θの方向に力を加えたとする。
このとき、物体が距離sだけ移動した場合、仕事WはFscosθである。

つまり、仕事は加えた力の「移動方向の成分」と「移動距離」の積で定義されるということだ。
どのような方向に力を加えても、仕事に寄与するのは「移動方向の成分」だけなのである。

移動方向に垂直に力を加えた場合、移動方向の成分は0である。
移動方向に垂直に力を加えても、それは仕事にならない。
これを具体的にいうと、円運動するときの向心力や、平面上をすべる物体の垂直抗力は仕事をしないということだ。

力を加える方向と仕事の関係をまとめると以下になる。

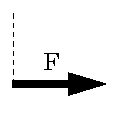
θ=0 Fと移動方向が同じ	0<θ<90	θ=90 Fと移動方向が直角
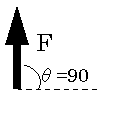W=Fs θ=0でWは最大	W=Fs cosθ	W=0 θ=90でWは最小

■次のページ：ベクトルの内積による定義

このページのTOPへ