慣性モーメント

慣性モーメントの計算方法

自転車を横に寝かせ、前輪を手で回転させるイメージだ。
軸の回転による抵抗や、スポークの質量は無視するとしよう。

ここでは、まず、リングの一部だけに注目してみよう。
この一部分の質量を⊿ｍとする。
これについて運動方程式を立てると次のようになる。
リング状の物体の場合

この式の展開を見ると、ケース１と同様の結果になったことが分かる。
加わった力のモーメントに比例した角加速度を生じるのだ。
その比例定数は⊿mr²であり、これが慣性モーメントということになる。

上記の計算では、リングを微少部分に分割して、その一部についての慣性モーメントを計算した。
リング全体の慣性モーメントを求めるためには、リング全周に渡って、各部分の慣性モーメントをすべて合算しなくてはならない。
これを式で表すと次のようになる。
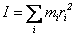
慣性モーメントの式

リング全体の質量をｍとすれば、この場合の慣性モーメントは
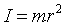
慣性モーメントの式
となる。

慣性モーメントIとはこのmr²のことである。
慣性モーメントがケース１とまったく同じ形になった。

くどいようだが、慣性モーメントは常にmr²になるとは限らない。

mr²が慣性モーメントの基本形であるが、軸の位置や質量の分布、形状によって様々なバリエーションがある。
例えば、次に説明するケース３「円盤状の物体を回転させる場合」では、mr²にならない。

2005/07/10