慣性モーメント

HOME＞ 剛体の力学＞慣性モーメント＞慣性モーメントの算出

慣性モーメントの計算方法

慣性モーメントの算出

どのような形状であっても慣性モーメントは以下の２ステップで算出する。
ステップ1: 回転体を微少部分に分割し、各微少部分の慣性モーメントを求める。
ステップ2: 各微少部分の慣性モーメントを、すべて合算する。

ここでは次のケースで慣性モーメントを算出してみよう。

ケース１	ケース２	ケース３
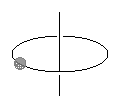
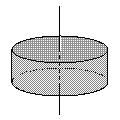
円運動する質点の場合	リング状の物体の場合	円柱型の物体の場合

上記のケース以外にも、様々な形状があり得ることは言うまでもない。
しかし、どんな場合であっても慣性モーメントは、2つのステップで計算するのが基本だ。

ケース1：質点を回転させる場合

穴の開いたビー玉に針金を通し、その針金でリングを作った状態をイメージすればいい。

リングを固定した状態で、質量ｍのビー玉を指で動かす場合を考えよう。
指がビー玉を動かす力Fは接線方向に作用している。

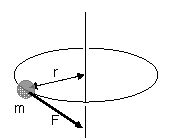
このときの運動方程式は次のようになる。

この式を見ると、加わった力のモーメントに比例した角加速度を生じることが分かる。
その比例定数はmr²だ。慣性モーメントIとはこのmr²のことである。
[..さらに詳しく見る..]

ケース2：リング状の物体の場合

この運動は自転車を横に寝かせ、前輪を手で回転させるイメージだ。

ここでは、まず、リングの一部だけに注目してみよう。
この一部分の質量を⊿ｍとする。
これについて運動方程式を立てると次のようになる。

この式の展開を見ると、ケース１と同様の結果になったことが分かる。
加わった力のモーメントに比例した角加速度を生じるのだ。
その比例定数は⊿mr²であり、これが慣性モーメントということになる。

上記の計算では、リングを微少部分に分割して、その一部についての慣性モーメントを計算した。
リング全体の慣性モーメントを求めるためには、リング全周に渡って、各部分の慣性モーメントをすべて合算しなくてはならない。
これを式で表すと次のようになる。

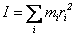
リング全体の質量をｍとすれば、この場合の慣性モーメントは

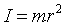
となる。
[..さらに詳しく見る..]

ケース3：円柱型の物体の場合

慣性モーメントは以下の２ステップで算出することはすでに述べた。
ステップ1: 回転体を微少部分に分割し、各微少部分の慣性モーメントを求める。
ステップ2: 各微少部分の慣性モーメントを、すべて合算する。

各微少部分は、それぞれ質点と見なすことができる。
だから、各微少部分の慣性モーメントは、ケース１で求めた質点を回転させた場合の慣性モーメントmr²と同等である。
どのような回転体であっても、微少部分に限定すれば、その部分の慣性モーメントはmr²になるのだ。

「mr²が慣性モーメントの基本形になる」というのは、「mr²」が各微少部分の慣性モーメントであるからにほかならない。

ケース１では、「質点を回転させた場合」という名目で算出したが、実は様々な回転体の各微少部分の慣性モーメントを求めていたのである。

この微少部分の慣性モーメントは、軸からの距離rに応じてそれぞれ異なる。
それらを、すべて積み上げて計算するので、軸の位置や質量の分布、形状により慣性モーメントは様々な形になるのである。

円柱型の物体(半径：R、質量：M、高さｈ)を回転させる場合で検証してみよう。
この円柱内に、円柱と同心の幅⊿rの薄い円筒を仮想する。
円筒は図中で色の濃い部分だ。

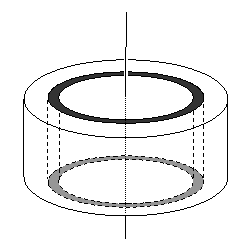
この円筒の質量m_iは、(円筒の体積) ÷(円柱の体積)×(円柱の質量)で求めることができる。

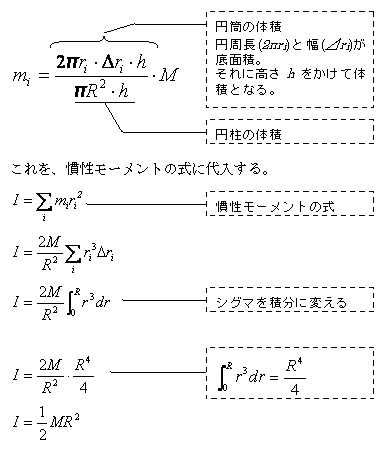
ここで式を見ると、高さhが入っていないことに気がつく。
円柱の慣性モーメントは、半径と質量によって決まり、高さは無関係なのだ。
高さのない(厚みのない)円盤であっても、同様である。
[..さらに詳しく見る..]

■次のページ：円運動している質点の慣性モーメント

このページのTOPへ