剛体の力学

慣性モーメント

慣性モーメントの意味

ここでは「回転しにくさ」の程度を示す物理量として慣性モーメントを解説しよう。
慣性モーメントの値が大きいほど、その物体は回転しにくい。
慣性モーメントは一般に記号Iで示され、並進運動における「慣性質量」に対応する。
単位は[kg・m²]である。

並進運動	動きにくさの指標	慣性質量(m)
回転運動	回転しにくさの指標	慣性モーメント(I)

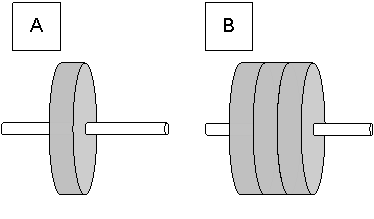
静止している金属製の円盤を回転させるとしよう。
Aの円盤は、金属板１枚分
Bの円盤は、金属板３枚分
である。

この場合、Bの方が回転させにくいことは直感でつかめると思う。
Bの方が回転させにくいのはなぜか？
Bの方が、慣性モーメントが大きいからである。

慣性モーメントは、回転しにくさの指標である。
力のモーメントに抗して、回転しまいとする能力と言ってもいい。

今度は上記の円盤A、Bがともに一定の角速度で回転しているとしよう。
これらを手で押さえて回転を停止させようとすると、どちらが楽に停止させられるであろうか？

この場合、Aの方が楽に停止でき、Bを停止させる方が大変であろうことは容易に想像できる。
これまた、Bの方が、慣性モーメントが大きいから停止しにくいのである。

慣性モーメントは、加わった力のモーメントに抗して、現在の角速度を維持しようとする能力でもある。

物体があればそれだけで慣性質量が決まる。
一方、慣性モーメントは、物体があるだけでは決まらない。

どこを軸にしてその物体を回すかによって、回転しやすい/しにくいは変わってくる。
つまり、回転軸の位置・方向に決めて初めて慣性モーメントが決まるのだ。
同じ物体でも回転軸の位置・方向によって慣性モーメントは変わってくるということだ。

試験に出題されやすい慣性モーメントのパターン

試験では、形状と回転軸を示した上で、「慣性モーメントを求めよ」という出題がよく見られる。
しかし、どのような形状であっても慣性モーメントは以下の２ステップで算出する。


ステップ1: 回転体を微少部分に分割し、各微少部分の慣性モーメントを求める。
ステップ2: 各微少部分の慣性モーメントを、すべて合算する。

試験対策で押さえておきたい、慣性モーメントの算出パターンは次の3つだ。
具体的な計算方法は慣性モーメントの算出で解説する。

ケース１	ケース２	ケース３
質点を回転させる場合	リング状の物体の場合	円柱型の物体の場合

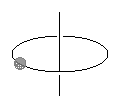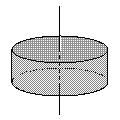上記のケース以外にも、様々な形状があり得ることは言うまでもない。
しかし、どんな場合であっても慣性モーメントは、2つのステップで計算するのが基本だ。

では、具体的な慣性モーメントの算出方法を見てみよう。

スポンサーリンク

2005/07/03

前ページ	このページの先頭	次ページ
物理の基礎基本・試験対策・レポート対策
物理学解体新書・HOME