慣性モーメント
平行軸の定理
剛体の慣性モーメントは、軸の位置・軸の方向ごとに異なる値になる。
これらに関し、重要な定理が二つある。
平行軸の定理と、直交軸の定理だ。
| 定理名 | 変数の意味 |
| 平行軸の定理 I=Ig+Md2 | Ig:質量中心を通る任意の軸のまわりの慣性モーメント I:この軸に平行な任意の軸のまわりの慣性モーメント M:質量 d:軸間距離 |
| 直交軸の定理 Iz=Ix+Iy | Ix:x軸のまわりの慣性モーメント Iy:y軸のまわりの慣性モーメント Iz:z軸のまわりの慣性モーメント |
ここでは、平行軸の定理を解説する。
まず、イメージを得るためにフリスビーを回転させるパターンを考えてみよう。
フリスビーを回転させるパターンは二つある。
| パターンA |
| 回転させながら投げる |
 |
| 回転軸はフリスビーの重心を通る |
| パターンB |
| 指先で回転させる |
 |
| 回転軸はフリスビーの縁を通る |
パターンAとパターンBとでは、回転軸が異なるので慣性モーメントが異なる。
そして回転軸が互いに平行であるに注目しよう。
重心を通る回転軸の周りの慣性モーメントIG(パターンA)と、これと平行な任意の軸の周りの慣性モーメントI(パターンB)には以下の関係がある。
この関係を平行軸の定理という。
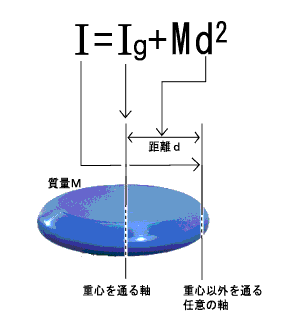
フリスビーの話で平行軸の定理のイメージがつかめたと思う。
ここから、数式を使って具体的に平行軸の定理の式を導きだしてみよう。
固定されたz軸に平行で、質量中心を通る軸をz'軸とする。
剛体を構成する任意の質点miのz軸のまわりの慣性モーメントをIとする。
miからz軸、z'軸に下ろした垂線の長さをh、h'とする。
垂線h'とdがつくる角をθとする。

■次のページ:直交軸の定理
スポンサーリンク
2005/07/03