運動の例
運動の例
世の中には多くの種類の運動がある。
それらの運動のパターンはすべて運動の3法則に集約される。
ここでは、様々な運動なかで、基本となるパターンを示そう。
| 等速直線運動 | どこまで行っても、同じ速度で進む運動を等速直線運動という。 |
| 等加速度直線運動 | 一定の加速度で、スピードアップしながら進む運動を等加速度直線運動という。 |
| 落体の運動 | 落下する物体は、常時重力が作用するので等加速度直線運動になる。 |
| 放物体の運動 | 水平方向には等速直線運動、鉛直方向には等加速度直線運動になる。 |
| 円運動 | 天体の公転などが、円運動である。常に中心に向けて力が作用する。これを中心力という。 |
| 単振動 | 円運動を真横から見た状態が単振動である。 |
| 単振り子 | 振れ角が小さい振り子は、単振動となる。 |
等速直線運動
スピードを変えず、一直線上を進む運動を等速直線運動という。
摩擦のない平面を物体がどこまでも滑っていく運動をイメージすればいい。
速度が一定なので、同じ時間に同じ距離を進む。
最初の1秒間に1メートル進んだら、次の1秒間も1メートル進む運動だ。

重力の影響を受けない宇宙空間を進む物体なども、等速直線運動の例となる。
「摩擦のない水平面上での運動」といった場合、「空気の抵抗や摩擦力など一切無視して計算する」といったことを示唆している。
いつまでも止まらないカーリングだと思えばいい。
物体が秒速v[m/s]で摩擦のない水平面上を運動している。
この物体には力が作用しないので、速度はv[m/s]のまま増減しない。
いつも等しい速度で、直線に進むのでこれを等速直線運動という。
この物体は、1秒後にv[m]、2秒後に2v[m]、3秒後に3v[m]の距離を進む。
速度が一定なので、速度と時間の積が距離になるのだ。
ここでは、微分方程式を用いていかにも学問らしく等速直線運動を記述するが、実態は小学校高学年で習う「速さ×時間=距離」の関係を用いて計算しているのに過ぎない。
[..等速直線運動の運動について、さらに詳しく見る]
等加速度直線運動
等速直線運動では、スピードを変えず一直線上を進む運動であった。
今度は、スピードを変えながら一直線上を進む運動について考えよう。
一定の割合でスピードを変えながら一直線上を進む運動を等加速度直線運動という。
スピードが上昇していく割合を加速度という。

[..等加速度直線運動の運動について、さらに詳しく見る]
落体の運動
ここでは、物体を落下させた場合の運動について考えよう。
落下する物体の運動は等加速度直線運動である。
落ちながら、だんだんとスピードを増していくのだ。

地球上の物体には、常時引力が作用している。
机の上に本が置いてあるとする。
この本には引力が作用してる。
一方で、机がこの引力と等大逆向きの抗力で本を押し返す。
引力と抗力の和がゼロなので、本は落ちもせず、浮き上がりもせず机の上に静止したままとなる。
落下する物体には、抗力が作用しない。引力だけが作用する。
落下中は引力だけが作用し続けるのだ。
力が作用すれば、加速度が生じる(運動の第二法則)
引力を受けたままの状態で落ち続けるので、落下の間常時加速度が生じることになる。
だから、落下物はだんだんとスピードを増してながら落下していくのだ。
地球の引力によって生じる加速度を重力加速度という。
重力加速度は、場所によって多少異なるがおおよそ9.8[m/s2]である。
月や火星に行けば、異なった値になる。
重力加速度は一般にgであらわす。
重力加速度は場所により異なるが、物体による違いはない。
つまり、重い物体も軽い物体も同じ加速度で落下するのだ。
物体は鉛直方向にgの加速度を受けつつ落下する。
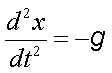
放物体の運動
物体が空中に投げられた状態であるとき、この物体を「放物体」という。
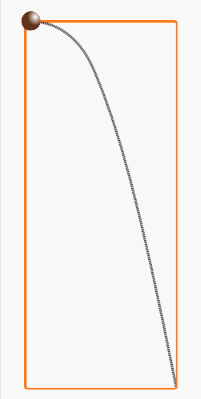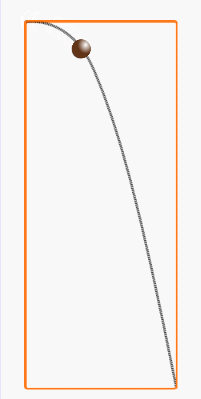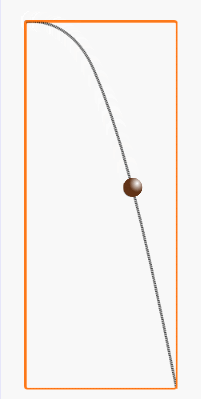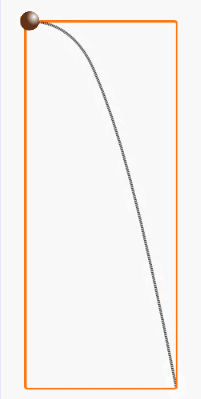
放物体が地面に落ちるまで通る道筋(軌跡)が放物線だ。
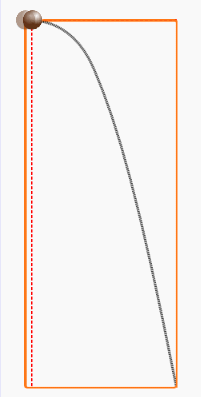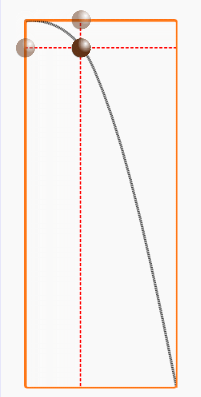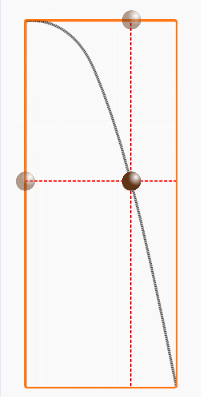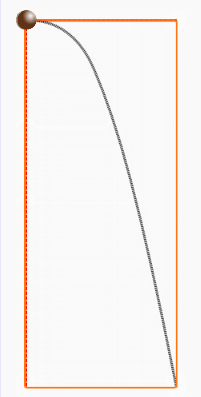
放物体の運動は、等速直線運動
と垂直落下運動の合成だ。
放物体の運動は、垂直方向と水平方向に分解して考えるのが定石だ。
垂直方向と水平方向それぞれにかかる力を明確にしよう。
垂直方向:重力
水平方向:なし(力は加わらない)
円運動

ひもの一方の端にボールを結びつけ、このひもの他端をもってこのボールを振り回したとしよう。
このとき、ボールが描く軌道は円形である。
このように円形の軌道を描く運動を円運動という。
惑星が太陽の周囲を公転する運動も円運動とみなしてよい。(実際は楕円軌道を描いているが)
[..円運動について、さらに詳しく見る]
単振動
バネに取り付いた錘(おもり)の往復運動が単振動だ。
往復運動の方向は、垂直であっても水平であっても、単振動に変わりはない。

単振動する錘(おもり)の特徴は3つある。
- 振動している間、錘の速度は刻々と変化する
- 振動の両端で、錘の速度は一度ゼロになり、運動の方向を折り返す
- 錘が振動の中央を通過するときのスピードが一番速い
バネを少し縮めるためには、少しの力が必要だ。
さらに、縮めるためには、さらに力が必要になる。
伸ばしても同じだ。伸ばせば伸ばすほど、より大きな力が必要になる。
このことから、バネが伸び縮みした長さと、バネが反発する力(バネ弾性力)は比例することが分かる。
これをフックの法則という。
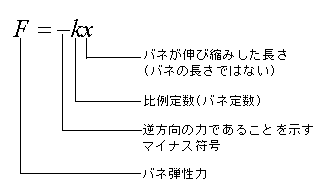
xは「バネの長さ」ではなく、「伸び縮みした長さ」だ。
元々5cmのバネが1cm縮んで4cmになった場合、x=1cmである。
x=5cmやx=4cmとするのは誤りである。
比例定数をバネ定数という。
単位長さを伸縮するのに必要な力を示している。
バネ定数の値が大きいほど、伸ばしにくい(縮めにくい)バネである。
バネ定数にマイナスが付いているのは、逆方向に力が生じる(反発する)ことを意味している。
この逆方向の力が、単振動の源泉となるのだ。
力は加速度と質量の積である。(ニュートンの第二法則)
錘の質量は一定なので、力(バネ弾性力)が最大のときに加速度も最大になる。
このことから、単振動の位置、速度、力、加速度を下表のようにまとめることができる。
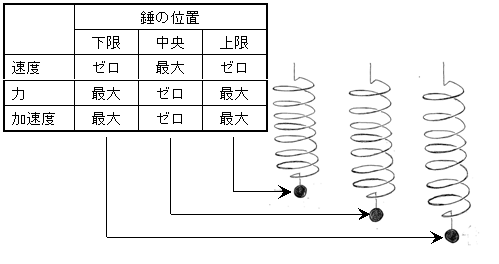
錘の移動に伴って、バネが縮み(伸び)バネ弾性力が増加する。
バネ弾性力がブレーキとなって錘が減速し、やがて停止し反転する。
この繰り返しが単振動なのだ。
錘の位置を時間tで2回微分すると錘の加速度が得られる。
この加速度と質量の積が力であり、バネ弾性力に相当する。
これを運動方程式で表すと次のようになる。
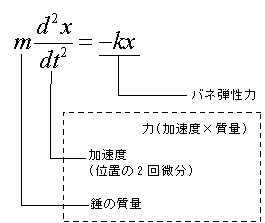
これが単振動の式を得るための微分方程式だ。
この式を見ると、「xを2回微分したらマイナスxになる」ということに気が付く。
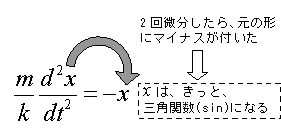
2回微分すると元の形にマイナスが付く関数は、sinだ。
このことから「単振動の式は三角関数になるに違いない」と見通すことができる。
質量m、バネ定数kを使用して、ω(オメガ)を以下のように定義しよう。
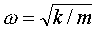
これを代入すると、次の式になる。
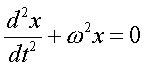
この式のパターンは微分方程式の基本形(線形2階微分方程式)だ。
A、αを定数とすると、この微分方程式の一般解は次の式になる。
つまり、これが単振動を表現する式なのだ。
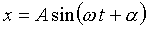
垂直に単振動するのであれば、重力mgも運動方程式に入るのではないかとう疑問もある。
その通り、重力mgも運動方程式に入れるべきなのだ。
ただし、重力とバネ弾性力がつりあった場所を原点(x=0)として単振動するので、結局、単振動の式は同じになるのである。
[..単振動について、さらに詳しく見る]
単振り子
糸を結んだ5円玉がユラユラ揺れている状態を想像して欲しい。
このユラユラ揺れている状態が単振り子である。

ひもの長さをl、ひもの下端の小球Aの質量をMとする。
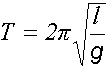
この式の中に登場するg(重力加速度)やπ(円周率)は定数なので人為的に値を変更できない。lのみが実験者の意思で変更可能である。
つまり周期Tは、「糸の長さのみ」で決まってしまうということだ。
小球Aの質量の大小や振幅は、周期には影響しない。
言い換えると、「周期を変えるには、糸の長さを変えるしかない」ということだ。
余談 |
上記は地球上に限定した話だ。 |
■次のテーマ:等速直線運動
スポンサーリンク
2005/06/03
2016/08/04
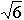 倍になる。(ゆっくり揺れる)
倍になる。(ゆっくり揺れる)